The main difference between RL and other types of machine learning, is that the learning procedure involves interactions between the agent and its environment.

The two main classes of RL approaches:

  • Model-free methods (direct)
  • Model-based methods (indirect)

The main difference between the two methods is whether a model of the interactions between the robot and the environment is employed:

  • Model-free: no model, trial-and-error.
  • Model-based: exist a model of the transition dynamics.
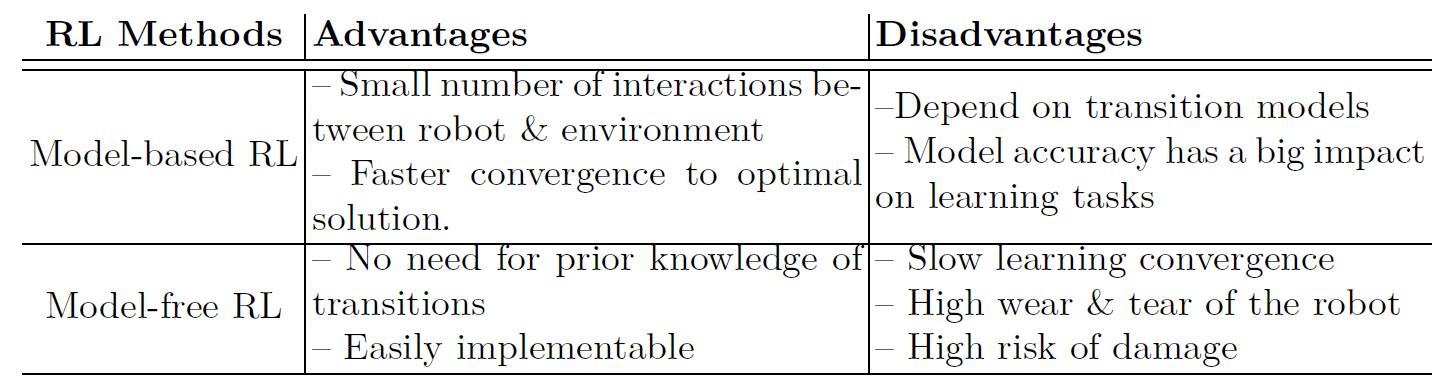
Advantages and disadvantages of Model-based and Model-free RL methods
Advantages and disadvantages of Model-based and Model-free RL methods
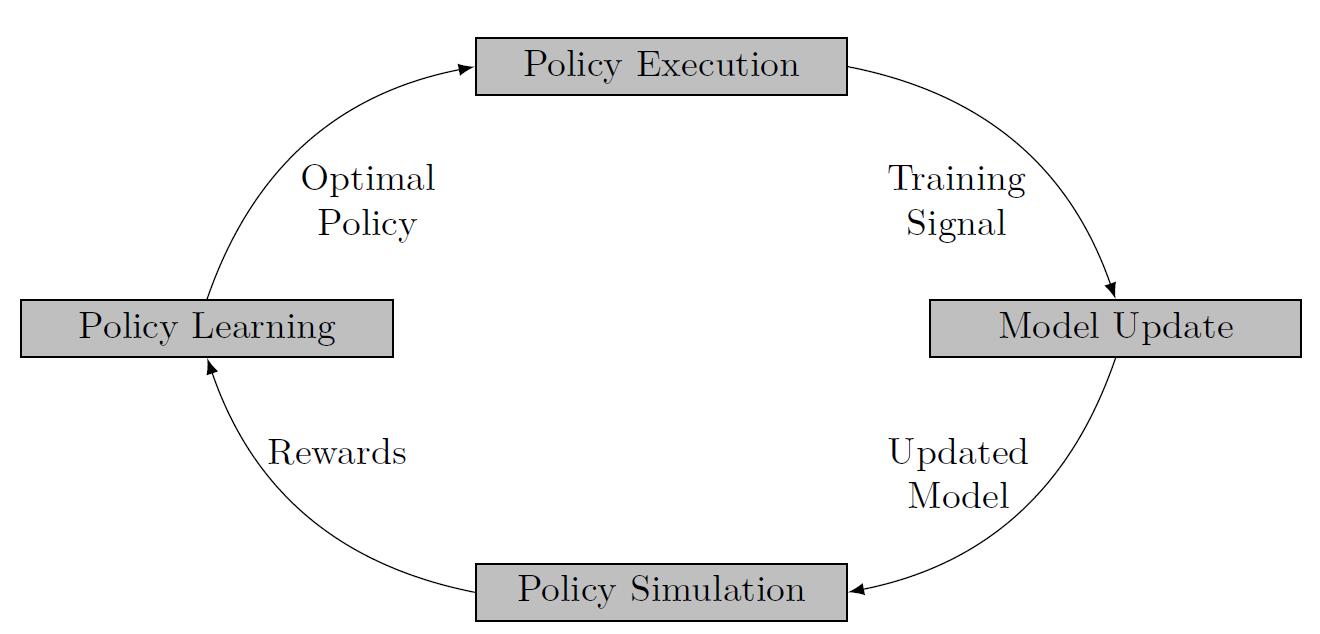
Pipeline of a Model-based RL algorithm
Pipeline of a Model-based RL algorithm

Methods for solving a Model-based RL problem

  • Value function approaches (\(V^{\pi}(s),Q^{\pi}(s,a)\))
    • Dynamic Programming (DP): require a model of the transition dynamics
      • Value Iteration
      • Policy Iteration
        • Policy evaluation
        • Policy improvement
    • Monte Carlo (MC): based on sampling
    • Temporal Difference Learning (TD): take into account the difference of the value function between two state transitions
      • SARSA
    • Differential Dynamic Programming (DDP)
      • LQR
  • Policy search methods: learn the optimal policy directly by modifying its parameters
    • Gradient-based methods: optimize the parameteried policy function by employing a gradient ascent approach
      • PILCO: require small amount of data for learning the policy, utilize Gaussian Process as a method for learning transtion dynamics
    • Expectation-Maximization (EM): maximizing the log-likelihood probability of the rewards
    • Sampling-based methods
      • PEGASUS (Policy Evaluation-of-Goodness And Search Using Scenarios)
    • Information Theory: exploit concepts such as entropy for the derivation of optimized policies
      • TRPO
    • Bayesian Optimization methods
    • Evolutionary computation
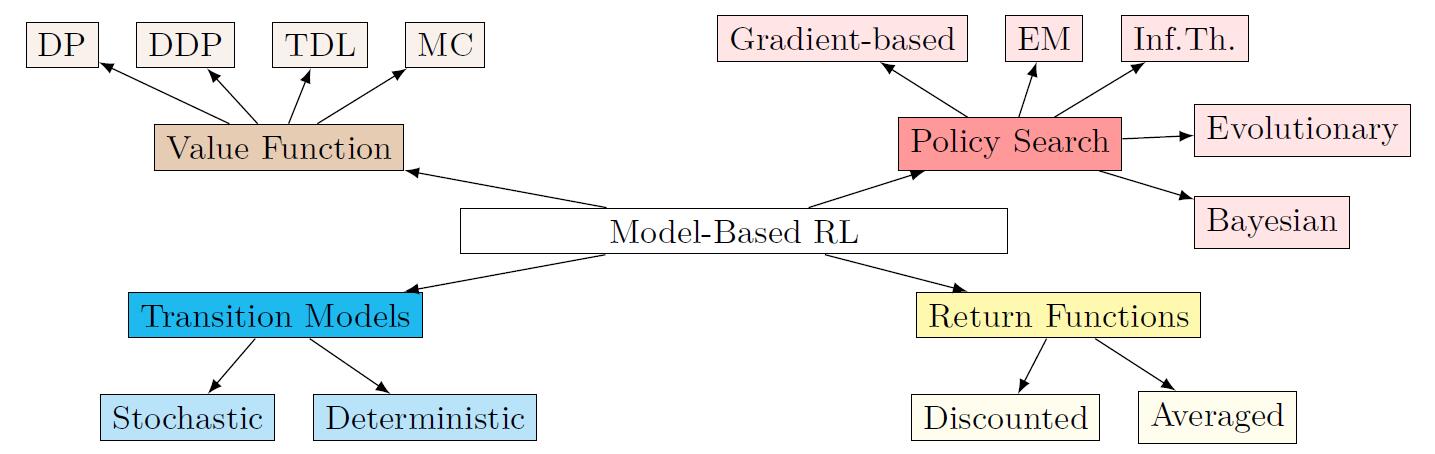
Approaches for solving a Model-based RL problem
Approaches for solving a Model-based RL problem

Value function methods

Bellman equations:

\[V^{\pi}(s) = \sum_a \pi (s,a) \sum_{s'} P(s' | s,a) [R(s,s',a) + \gamma V^{\pi} (s')]\] \[Q^{\pi} (s,a) = \sum_{s'} P(s' | s,a) [R(s,s',a) + \gamma Q^{\pi} (s',a')]\]

Bellman Optimality equations:

\[V^{\pi_*}(s) = max_{a \in A(s)} \sum_{s'} P(s' | s,a) [R(s,s',a) + \gamma V^{\pi_*}(s')]\] \[Q^{\pi_*}(s) =\sum_{s'} P(s' | s,a) \left[ R(s,s',a) + \gamma max_{a'} Q^{\pi_*}(s',a') \right]\]

Transition Models

\[P(s,a) \mapsto s'\]

Transition models have a large impact on the performance of model-based RL algorithms since the policy learning step relies on the accuracy of their predictions.

Classes of the transition models

  • Deterministic models
  • Stochastic models
    • Gaussian Processes (GP)

References