Cross Entropy

Entropy

假设\(X\)是一个离散型随机变量，概率分布函数为\(p(x) = P(X = x)\)，定义事件\(X = x_0\)的信息量为：

\[I(x_0) = - \log(p(x_0)).\]

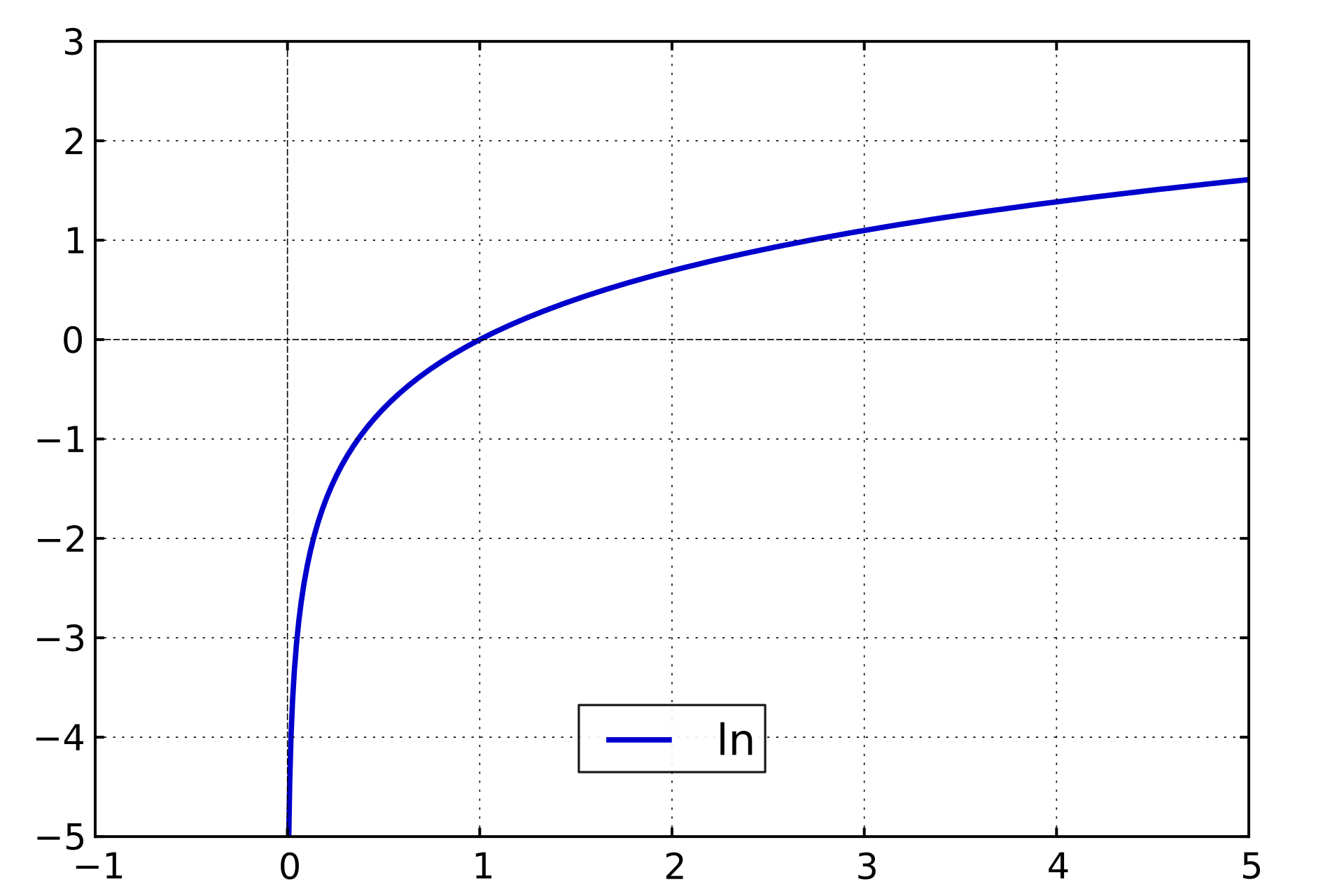
一个事件发生的概率越大，则它携带的信息量就越小：

  • 当\(p(x_0)=0.1\)时，\(I(x_0)=3.3219\)
  • 当\(p(x_0)=0.999\)时，\(I(x_0)=0.0014\)
  • 当\(p(x_0)=1\)时，\(I(x_0)=0\)

度量概率分布的不确定度称为熵，对所有可能结果带来的信息量求期望，即可得到熵。

如：小明的考试结果是一个0-1分布，\(p(X=1)=0.1\)，则其熵为：

\[H(x) = - [p(X=1) \log(p(X=1))+(1-p(X=1)) \log(1-p(X=1))] = 0.4690.\]

0-1分布的熵与概率之间的关系为：

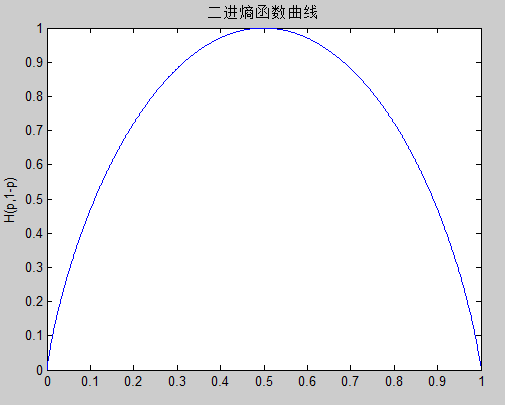
对于一个随机变量\(x\)，它的所有可能取值的信息量的期望\(E(I(x))\)就称为熵:

\[H(x) = E[I(x)] = E[-\log(p(x))] = E[\log \frac{1}{p(x)}] = - \sum_{x \in X} p(x) \log p(x).\]

熵的单位：

  • 比特(bit)：当log底数为2时。
  • 奈特：当log底数为e时。

Relative Entropy

相对熵又称为KL散度，是两个随机分布之间距离的度量：

\[\begin{aligned} D_{KL}(p \Vert q) & = E[\log \frac{p(x)}{q(x)}] \\ & = \sum p(x) \log \frac{p(x)}{q(x)} \\ & = \sum [p(x)\log p(x) - p(x) \log q(x)] \\ & = - H(p) - \sum p(x) \log q(x) \\ & = - H(p) + E_p[-\log q(x)] \\ & = H_p(q) - H(p). \end{aligned}\]

为了保证连续性，约定：

\[0\log \frac{0}{0} = 0, 0 \log \frac{0}{q} = 0, p \log \frac{p}{0} = \infty.\]

其中，\(H_p(q)\)表示在\(p\)分布下，使用\(q\)进行编码所需要的bit数，而\(H(p)\)表示真实分布\(p\)所需要的最小编码bit数，因此相对熵即为在真实分布的前提下，使用\(q\)分布进行编码相对于真是分布编码所多出的bit数。

Cross Entropy

交叉熵是信息论中的概念，主要用于度量两个概率分布之间的差异性信息。给定两个概率分布\(p\)和\(q\)，通过\(q\)来表示\(p\)的交叉熵为：

\[H(p,q) = - \sum_x p(x) \log q(x) = H(p) + D_{KL}(p \Vert q).\]

交叉熵与相对熵只相差了\(H(p)\)，当\(p\)已知时，\(H(p)\)为常数，此时交叉熵和相对熵在行为上是等价的，都反映了两个分布之间的相似程度。

注：交叉熵表示的是两个概率分布之间的距离（或可以说是通过概率分布\(q\)来表示概率分布\(p\)的困难程度），\(p\)代表真实值，\(q\)代表预测值，交叉熵越小，两个概率分布越接近。

用于神经网络中的 Loss Function

在神经网络中，将前向传播得到的输出预测值转化成概率分布并与真实值的概率分布进行交叉熵运算，如何转化成概率分布呢？

输出预测值的概率分布

通过softmax函数进行转化：（所以交叉熵和softmax函数经常一起使用）

\[softmax(y)_i = \frac{e^{y_i}}{\sum_{j=1}^n e^{y_j}},\]

其中，神经网络的输出预测值为：\(y_1,y_2,\cdots,y_n\)。

真实值的概率分布

对于分类问题，通过对真实label进行one-hot编码，如：标签4可以表示为[0,0,0,0,1,0,0,0,0,0]，从而得到真实值的概率分布。

Mean Squared Error (MSE)

在逻辑回归问题中，常常使用MSE作为loss function：

\[loss = \frac{1}{2m} \sum_{i=1}^m (y_i - y_{i\_})^2.\]

其中，\(y_i\)表示期望输出，\(y_{i\_}\)表示实际输出，\(m\)表示样本数。

在分类问题中，MSE不适用，因为经过softmax函数之后的输出预测值与真实值的MSE函数是非凸函数，梯度下降算法很难保证达到全局最优解。而Cross Entropy作为loss function时，具有单调性，loss越大，梯度越大，因此分类问题一般采用交叉熵作为loss function。

Hinge Loss

  • Hinge loss is a loss function used for training classifiers.
  • Used for maximum-margin classification, most notably for support vector machines (SVMs).
  • 与PPO算法中的Clip推导有一定的关联。

The hinge loss of the prediction \(y\) is defined as:

\[L(y) = \max(0, 1 - t\cdot y),\]

where

  • \(t = \pm 1\) is the intended output.
  • \(y\) is the classifier score, it should be the raw output of the classifier’s decision function, not the predicted class label.

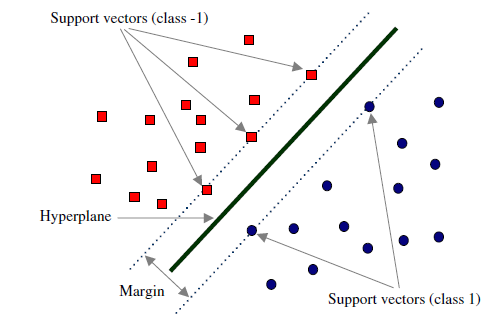
当\(t\)和\(y\)符号相同，且\(\vert y\vert \ge 1\)时，Hinge Loss \(L(y) = 0\);

当\(t\)和\(y\)符号相同，且\(\vert y\vert < 1\)时，Hinge Loss \(L(y) > 0\)，预测正确，但没有足够的边缘;

当二者符号相反时，Hinge Loss随着\(\vert y\vert\)的增大而增大。

References