Rotation Matrix

2D Rotation

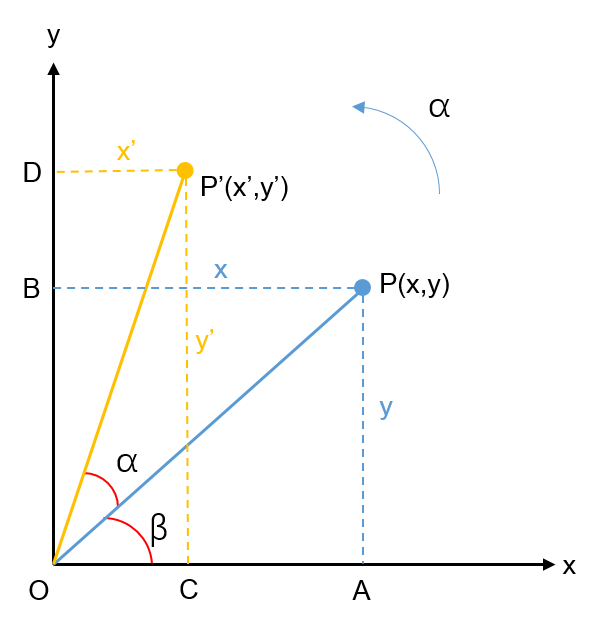
From \(P(x,y)\) to \(P'(x',y')\), let \(r = OP = OP'\):

\[x = r\cos\beta, y = r\sin\beta.\] \[x' = r\cos(\alpha+\beta) = r(\cos\alpha\cos\beta - \sin\alpha\sin\beta) = x \cos\alpha - y \sin\alpha,\] \[y' = r\sin(\alpha+\beta) = r(\sin\alpha\cos\beta + \cos\alpha\sin\beta) = x \sin\alpha + y \cos\alpha.\]

Thus,

\[\left[ \begin{matrix} x' \\ y' \end{matrix} \right] = \left[ \begin{matrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{matrix} \right] \left[ \begin{matrix} x \\ y \end{matrix} \right].\]

3D Rotation

Rotate \(\psi\) around \(Z\) axis

\[\left[ \begin{matrix} x' \\ y' \\ z' \end{matrix} \right] = \left[ \begin{matrix} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ z \end{matrix} \right].\]

Rotate \(\theta\) around \(Y\) axis

\[\left[ \begin{matrix} x' \\ y' \\ z' \end{matrix} \right] = \left[ \begin{matrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ z \end{matrix} \right].\]

Rotate \(\phi\) around \(X\) axis

\[\left[ \begin{matrix} x' \\ y' \\ z' \end{matrix} \right] = \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi & \cos\phi \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ z \end{matrix} \right].\]

Then, the rotation matrix can be obtained as follows:

从世界坐标系按照$Z\to Y\to X$旋转的顺序，旋转到机体坐标系。

\[R = R_Z(\psi) R_Y(\theta) R_X(\phi) = \left[ \begin{matrix} \cos\psi\cos\theta & \quad \cos\psi\sin\theta\sin\varphi - \sin\psi\cos\varphi &\quad \cos\psi \sin\theta\cos\varphi + \sin\psi\sin\varphi \\ \sin\psi\cos\theta & \quad \sin\psi\sin\theta\sin\varphi + \cos\psi\cos\varphi & \quad \sin\psi \sin\theta\cos\varphi - \cos\psi\sin\varphi \\ -\sin\theta & \quad \cos\theta\sin\varphi & \quad \cos\theta\cos\varphi \end{matrix} \right].\]

因此，机体坐标系上的点$A$，在世界坐标系下的位置为：$RA$.

Euler Angles

Roll \(\phi\)

Pitch \(\theta\)

Yaw \(\psi\)

Gimbal Lock

Quaternion

Definition

\[\mathbf{q} = w + x i + y j + z k = \begin{bmatrix} w \\ x \\ y \\ z \end{bmatrix}.\]

Pure quaternion: \(\mathbf{q} = [0, x, y, z]\).

Using quaternion to describe the rotation around vector \(K = (K_x, K_y, K_z)\) with angle \(\theta\):

\[(w,x,y,z) = \left( \cos\frac{\theta}{2}, K_x \sin\frac{\theta}{2}, K_y \sin\frac{\theta}{2}, K_z \sin\frac{\theta}{2} \right),\] \[w^2 + x^2 + y^2 + z^2 = 1.\]

Inverse

\[\mathbf{q}^{-1}\mathbf{q} = \mathbf{q}\mathbf{q}^{-1} = 1.\]

Conjugate

\[\mathbf{q}^* = w - xi-yj-zk.\] \[\mathbf{q}\mathbf{q}^* = \lVert\mathbf{q}\rVert^2.\] \[\mathbf{q}^{-1} = \frac{\mathbf{q}^*}{\lVert\mathbf{q}\rVert^2}.\]

Relationship between them

From Quaternion to Euler Angles

\[\begin{aligned} \phi & = atan2(2(wx + yz), 1-2(x^2+y^2)), \\ \theta & = asin(2(wy - xz)), \\ \psi & = atan2(2(wz+xy), 1-2(y^2+z^2)). \end{aligned}\]

Also, you can see the animated demo of the relationship between quaternion and Euler angles here.

From Euler Angles to Quaternion

\[\mathbf{q} = \left[ \begin{matrix} w \\ x \\ y \\ z \end{matrix} \right] = \left[ \begin{matrix} \cos\left( \frac{\phi}{2} \right)\cos\left( \frac{\theta}{2} \right)\cos\left( \frac{\psi}{2} \right) + \sin\left( \frac{\phi}{2} \right)\sin\left( \frac{\theta}{2} \right)\sin\left( \frac{\psi}{2} \right) \\ \sin\left( \frac{\phi}{2} \right)\cos\left( \frac{\theta}{2} \right)\cos\left( \frac{\psi}{2} \right) - \cos\left( \frac{\phi}{2} \right)\sin\left( \frac{\theta}{2} \right)\sin\left( \frac{\psi}{2} \right) \\ \cos\left( \frac{\phi}{2} \right)\sin\left( \frac{\theta}{2} \right)\cos\left( \frac{\psi}{2} \right) + \sin\left( \frac{\phi}{2} \right)\cos\left( \frac{\theta}{2} \right)\sin\left( \frac{\psi}{2} \right) \\ \cos\left( \frac{\phi}{2} \right)\cos\left( \frac{\theta}{2} \right)\sin\left( \frac{\psi}{2} \right) - \sin\left( \frac{\phi}{2} \right)\sin\left( \frac{\theta}{2} \right)\cos\left( \frac{\psi}{2} \right) \end{matrix}\right].\]

From Euler Angles to Rotation Matrix

\[R = R_Z(\psi) R_Y(\theta) R_X(\phi) = \left[ \begin{matrix} \cos\psi\cos\theta & \quad \cos\psi\sin\theta\sin\varphi - \sin\psi\cos\varphi &\quad \cos\psi \sin\theta\cos\varphi + \sin\psi\sin\varphi \\ \sin\psi\cos\theta & \quad \sin\psi\sin\theta\sin\varphi + \cos\psi\cos\varphi & \quad \sin\psi \sin\theta\cos\varphi - \cos\psi\sin\varphi \\ -\sin\theta & \quad \cos\theta\sin\varphi & \quad \cos\theta\cos\varphi \end{matrix} \right].\]

From Rotation Matrix to Euler Angles

\[R = \left[ \begin{matrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{matrix} \right],\] \[\begin{aligned} \phi & = atan2(r_{32}, r_{33}), \\ \theta & = atan2(-r_{31}, \sqrt{r_{32}^2 + r_{33}^2}), \\ \psi & = atan2(r_{21},r_{11}). \end{aligned}\]

From Quaternion to Rotation Matrix

\[R = \left[\begin{matrix} 1-2(y^2+z^2) & 2(xy-wz) & 2(xz+wy) \\ 2(xy+wz) & 1-2(x^2+z^2) & 2(yz-wx) \\ 2(xz-wy) & 2(yz+wx) & 1-2(x^2+y^2) \end{matrix}\right].\]

From Rotation Matrix to Quaternion

\[\begin{aligned} w & = \frac{\sqrt{tr(R)+1}}{2}, \\ x & = \frac{r_{32}-r_{23}}{4w}, \\ y & = \frac{r_{13}-r_{31}}{4w}, \\ z & = \frac{r_{21}-r_{12}}{4w}. \end{aligned}\]

Where \(tr(R) = r_{11}+r_{22}+r_{33}\).