Path Planning VS Trajectory Planning VS Motion Planning

The difference between PP, TP and MP
Index Path Planning Trajectory Planning Motion Planning
Dimension Space Space + Time Space + Time
Constraints Kinematics Kinematics + Dynamics (balance, joint limits, torque bounds, velocity/acceleration/jerk limits) Kinematics + Dynamics + Environments (collision avoidance)
Process Planning + Waypoints Planning + Generation Planning + Generation + Controller
Output Path Path + Speed (Acceleration, Jerk) Discrete Motions / Commands

Challenges

  1. How to define the optimal trajectory?
    • cost function
      • energy consumption
    • objective function
      • travel length
  2. Optimization methods:
    • discrete method
      • search-based
      • sampling-based
    • continuous method
      • optimization-based
  3. Constraints:
    • dynamics limits
    • kinematic limits
    • obstacle avoidance
  4. Trajectory optimization:
    • smoothness
    • consider uncertainty

Trajectory Planning

  • Known as a movement from starting point to ending point by satisfying the constraints along the path.
  • It is an essential part of robot motion planning.
  • Planning high-speed trajectories for UAV in unknown environments requires:
    • fast algorithms able to solve the trajectory generation problem in real-time in order to be able to react quickly to the changing knowledge of the world and that guarantee safety at all times.
    • Dynamical feasible:
      • Satisfy the physical limits.
      • The underactuated nature of the quadrotor.

Trajectory Generation


Top: Power Loop, Barrel Roll, Matty Flip, Bottom: Combo.

A. Loquercio, E. Kaufmann, and D. Scaramuzza, “Deep Drone Acrobatics,” RSS Robot. Sci. Syst., 2020.

Instead of directly planning in the full state space, generating the trajectory in the space of flat outputs:

\[\sigma = [p_x,p_y,p_z,\psi]^T.\]

It can be shown that any smooth trajectory in the space of flat outputs can be tracked by the underactuated platform.

Polynomial trajectory

Motivation

Consider the problem of navigating through \(m\) keyframes (waypoints) at specified times.

In between each keyframe there is a safe corridor that the quadrotor must stay within.

We can use straight lines to interpolate between keyframes. However, the trajectory is inefficient because it has infinite curvature at the keyframes, which requires the quadrotor to come to a stop at each keyframe.

Polynomial functions can fit out an optimal trajectory that smoothly transitions through the keyframes at the given times while staying within safe corridors.

Constraints of the trajectory

Enforce some limits when designing a trajectory:

  • Maximum Speed: \(v_{max}\).
  • Maximum Collective thrust: \(F_{T_{max}}\).
  • Maximum norm of the roll and pitch rates: \(\omega_{max}\).

The limits of the trajectory need to be computed from a desired state sampled from the given trajectory:

\[s_{des} = [p_{des} \quad v_{des} \quad a_{des} \quad j_{des}].\]

Speed

\[v = \lVert v_{des} \rVert.\]

Collective thrust

\[F_T = \lVert a_{des} - g \rVert.\]

The norm of the roll and pitch rates

In world frame,

\[F = a_{des} - g = R\cdot \mathbf{F_T}.\]

Then,

\[\bar{F} = \frac{F}{\lVert F \rVert} = R\cdot\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}.\]

Take the derivative:

\[\dot{\bar{F}} = \dot{R} \cdot\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = R \hat{\omega}\cdot\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}.\]

Then,

\[\hat{\omega}\cdot\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = R^T \dot{\bar{F}},\] \[\begin{bmatrix} \omega_y \\ -\omega_x \\ 0 \end{bmatrix} = R^T\dot{\bar{F}}.\]

Where

\[\dot{\bar{F}} = \frac{d}{dt}\left( \frac{F}{\lVert F \rVert} \right) = \frac{\dot{F}\lVert F \rVert - F\frac{F^T \dot{F}}{\lVert F \rVert}}{\lVert F \rVert^2} = \frac{\dot{F}}{\lVert F\rVert} - \frac{FF^T\dot{F}}{\lVert F\rVert^3} = \frac{j}{\lVert F\rVert} - \frac{FF^Tj}{\lVert F\rVert^3}.\]

Thus,

\[\begin{aligned} \begin{bmatrix} \omega_y \\ -\omega_x \\ 0 \end{bmatrix} & = R^T \left( \frac{j}{\lVert F\rVert} - \frac{FF^Tj}{\lVert F\rVert^3} \right) \\ & = R^T \frac{j}{F_T} - R^T\frac{R\mathbf{F_T} \mathbf{F_T}^T R^T j}{F_T^3} \\ & = R^T \frac{j}{F_T} - \frac{\mathbf{F_T} \mathbf{F_T}^T R^T j}{F_T^3}. \end{aligned}\]

Where

\[\mathbf{F_T} \mathbf{F_T}^T = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & F_T^2 \end{bmatrix}.\]

Then,

\[\begin{bmatrix} \omega_y \\ -\omega_x \\ 0 \end{bmatrix} = \begin{bmatrix} x_B^T\cdot \frac{j}{F_T} \\ y_B^T\cdot \frac{j}{F_T} \\ z_B^T\cdot \frac{j}{F_T} \end{bmatrix} - \begin{bmatrix} 0 \\ 0 \\ z_B^T \cdot \frac{j}{F_T} \end{bmatrix}.\] \[\lVert R^T \cdot \frac{j}{F_T}\rVert = \lVert\frac{j}{F_T}\rVert.\] \[z_B = \frac{a_{des} - g}{\lVert a_{des} - g\rVert}.\]

Therefore, the norm of the roll and pitch body rates:

\[\lVert \omega_{x,y}\rVert = \left\Vert \begin{bmatrix} \omega_y \\ -\omega_x \\ 0 \end{bmatrix} \right\Vert = \sqrt{\left\Vert \frac{j}{F_T} \right\Vert^2 - \left( z_B^T\frac{j}{F_T} \right)^2}.\]

Polynomial Coefficients

The goal of polynomial trajectory generation is to obtain the polynomial coefficients which satisfy some constraints.

A piecewise-smooth trajectory can be generated by piecewise polynomial functions of order \(n\) over \(m\) keyframes time intervals (\(m\) segments, add the start state):

\[\sigma(t) = \begin{cases} \sum_{i=0}^n \sigma_{i,1} t^i & t_0 \le t < t_1 \\ \sum_{i=0}^n \sigma_{i,2} t^i & t_1 \le t < t_2 \\ \vdots \\ \sum_{i=0}^n \sigma_{i,m} t^i & t_{m-1} \le t \le t_{m}. \end{cases}\]

Write as matrix form:

\[\sigma(t) = \begin{cases} \sigma_1\cdot [1,t,t^2,\cdots,t^n] & t_0 \le t < t_1 \\ \sigma_2\cdot [1,t,t^2,\cdots,t^n] & t_1 \le t < t_2 \\ \vdots \\ \sigma_m\cdot [1,t,t^2,\cdots,t^n] & t_{m-1} \le t \le t_{m}. \end{cases}\]

Where \(\sigma^j, j = \{1,\cdots,m\}\) is the polynomial coefficient matrix (\(4\times (n+1)\)) of the \(j\)th piecewise trajectory.

For each piecewise trajectory polynomial:

\[\sigma(t) = \sigma_{4\times (n+1)} \cdot [1,t,t^2,\cdots,t^n].\]

Then, for anytime \(t\), the position \(p_t\), velocity \(v_t\), acceleration \(a_t\), jerk \(j_t\), and snap of the trajectory can be calculated by:

\[\begin{aligned} p_t & = \sigma_{3\times (n+1)} \cdot [1,t,t^2,t^3,t^4,t^5,\cdots,t^n], \\ v_t & = \sigma_{3\times (n+1)} \cdot [0,1,2t,3t^2,4t^3,5t^4,\cdots,nt^{n-1}], \\ a_t & = \sigma_{3\times (n+1)} \cdot [0,0,2,6t,12t^2,20t^3,\cdots,n(n-1)t^{n-2}], \\ j_t & = \sigma_{3\times (n+1)} \cdot [0,0,0,6,24t,60t^2,\cdots,\frac{n!}{(n-3)!}t^{n-3}], \\ snap_t & = \sigma_{3\times (n+1)} \cdot [0,0,0,0,24,120t,\cdots,\frac{n!}{(n-4)!}t^{n-4}]. \end{aligned}\]

Minimum Snap Trajectory

Why minimize snap?1

  • Minimizing the control effort, do this indirectly by minimizing snap.
  • The thrusts is related to the second derivatives of the curve.
  • The torques of control inputs appear as functions of the fourth derivatives of the positions.
  • Minimizing snap will give us the curve that requires the least reorientation of the quadrotor along it, and will guarantee smoothness.

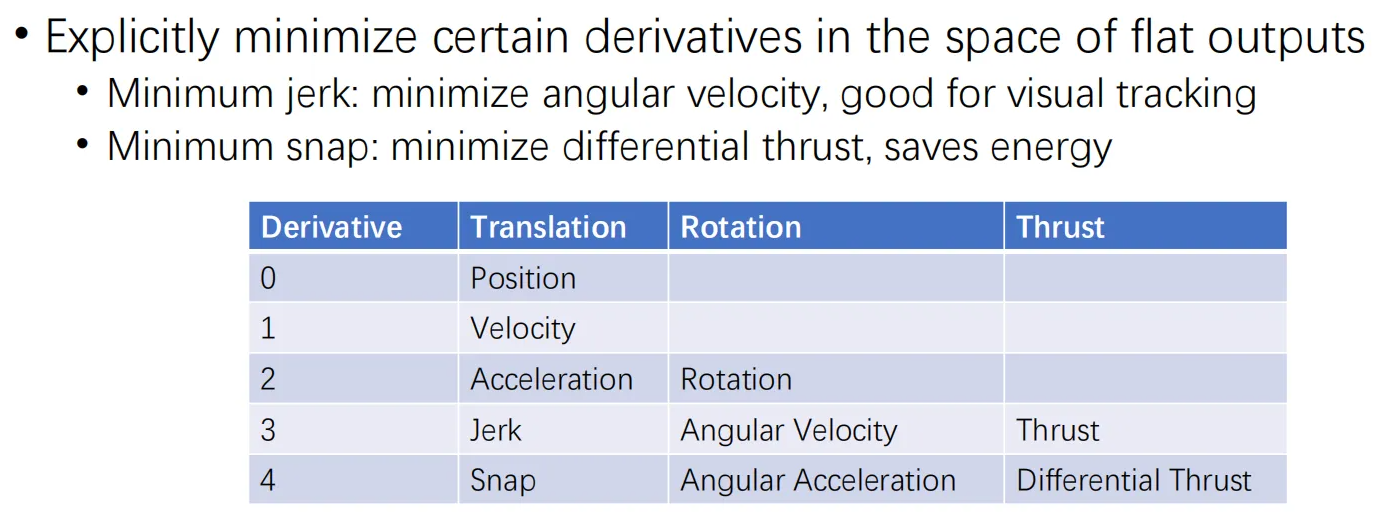
The optimization program to solve this problem:

  • Minimize the integral of the \(k_p\)th derivative of position squared.
    • \(k_p = 4\), minimize the integral of the square of the norm of the snap.
  • Minimize the integral of the \(k_\psi\)th derivative of yaw angle squared.
    • \(k_\psi = 2\).

Cost function:

\[\min \int_{t_0}^{t_{m}} \mu_p \left\Vert \frac{d^{k_p}p_t}{dt^{k_p}}\right\Vert^2 + \mu_\psi \left\Vert \frac{d^{k_\psi}\psi_t}{dt^{k_\psi}}\right\Vert^2 dt,\] \[s.t. \begin{cases} \sigma(t_i) = \sigma_i & i = 0,\cdots, m \\ \frac{d^k p_t}{dt^k}\vert_{t = t_j} = 0 \text{ or free} & j = 0,m; k = 1,\cdots,k_p \\ \frac{d^k \psi_t}{dt^k}\vert_{t = t_j} = 0 \text{ or free} & j = 0,m; k = 1,\cdots,k_\psi. \end{cases}\]

where

  • \(\mu_p,\mu_\psi\) are constants that make the integrand nondimensional.

Formulate the problem as a quadratic program (QP) by:

\[\sigma_{i,j} = [x_{i,j},y_{i,j},z_{i,j},\psi_{i,j}]^T,\] \[\min \sigma_{i,j}^T H \sigma_{i,j} + f^T \sigma_{i,j},\] \[s.t. \quad A\sigma_{i,j} \le b.\]

For minimize snap:

\[\begin{aligned} \min \int_{t_0}^{t_m} (snap_t)^2 dt & = \min \sum_{j=1}^m \int_{t_{j-1}}^{t_j}(snap_t)^2 dt \\ & = \min \sum_{j=1}^m \int_{t_{j-1}}^{t_j} \left[ \left( \sigma_{3\times (n+1)}^j \cdot[0,0,0,0,24,120t,\cdots,\frac{n!}{n-4!}t^{n-4}] \right) \left( \sigma_{3\times (n+1)}^j \cdot[0,0,0,0,24,120t,\cdots,\frac{n!}{n-4!}t^{n-4}] \right)^T \right] dt \\ & = \min \sum_{j=1}^m \sigma_{3\times(n+1)}^j \int_{t_{j-1}}^{t_j} \left[ \left( [0,0,0,0,24,120t,\cdots,\frac{n!}{n-4!}t^{n-4}] \right) \left( [0,0,0,0,24,120t,\cdots,\frac{n!}{n-4!}t^{n-4}] \right)^T \right] dt \left(\sigma_{3\times(n+1)}^j\right)^T \\ & = \min \sum_{j=1}^m \sigma_{3\times(n+1)}^j Q_j \left(\sigma_{3\times(n+1)}^j\right)^T \\ & = \min \sum_{j=1}^m \sigma_{3\times(n+1)}^j \begin{bmatrix} 0_{4\times4} & 0_{4\times(n-3)} \\ 0_{(n-3)\times 4} & \frac{r!}{(r-4)!}\frac{c!}{(c-4)!}\frac{1}{(r-4)+(c-4)+1}\left( t_j^{r+c-7} - t_{j-1}^{r+c-7} \right) \end{bmatrix} \left(\sigma_{3\times(n+1)}^j\right)^T. \end{aligned}\]

Where \(r,c\) are the index of row and column.

Constraints:

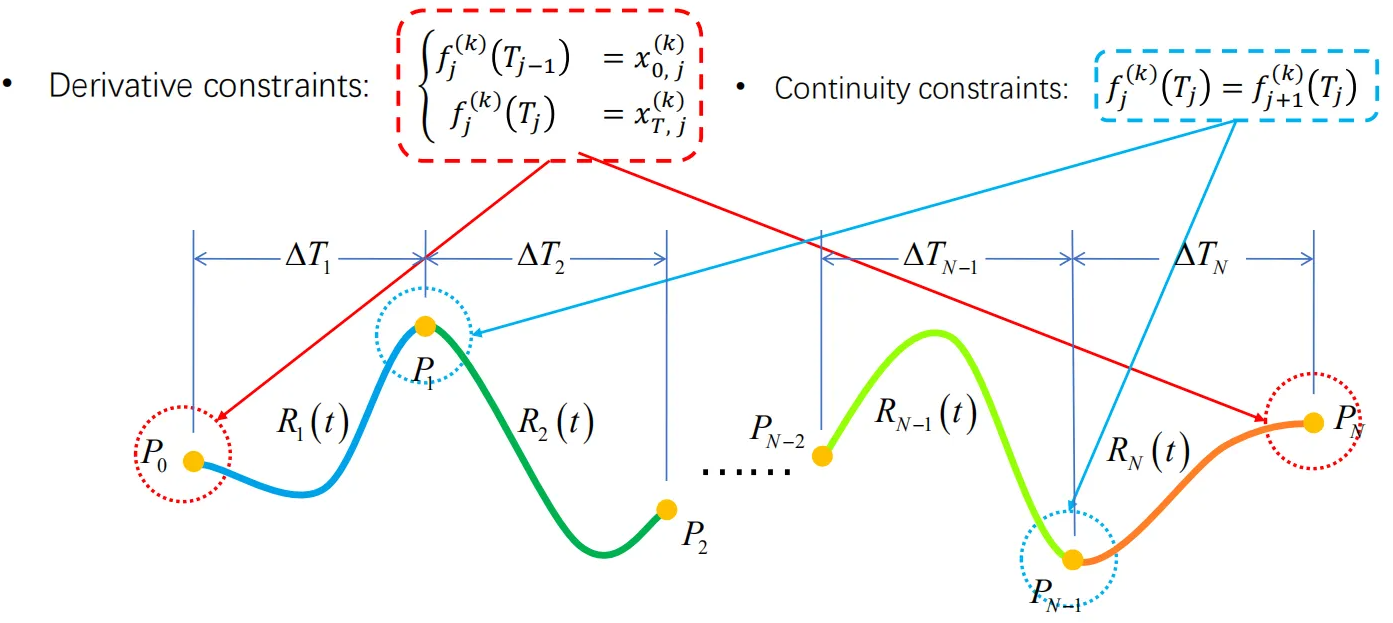
  • Equality constraints.
    • At \(t_0\):
      • \(\sigma_{3\times (n+1)} \cdot [1,t_0,t_0^2,t_0^3,t_0^4,t_0^5,\cdots,t_0^n] = p_0\).
      • Also, \(v_0,a_0,j_0\).
    • Similar, \(p_k,v_k,a_k\).
  • Inequality constraints.
    • Used in corridor environment.
    • \(p_k \le p_{max}\).
    • Similar, \(v_k,a_k\).

Then, using QP solver (Lagrangian method) to calculate the polynomial coefficients.

Add corridor constraints

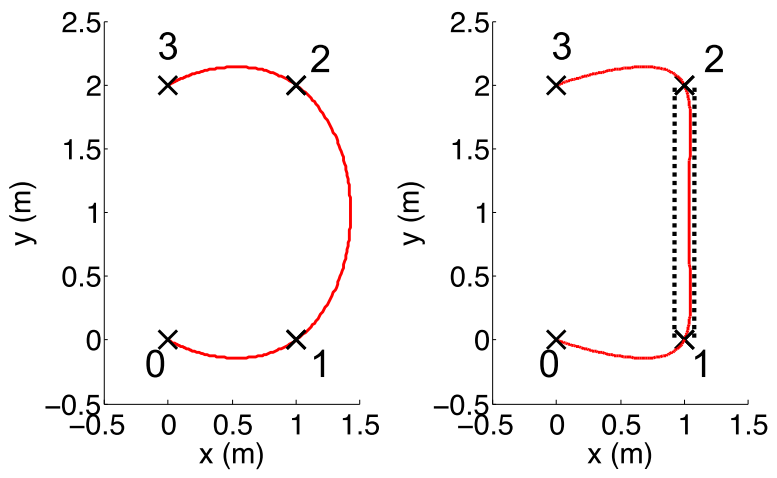
Define the unit vector along the segment from \(\mathbf{p}_j\) to \(\mathbf{p}_{j+1}\) as:

\[\mathbf{N}_j = \frac{\mathbf{p}_{j+1} - \mathbf{p}_j}{\Vert \mathbf{p}_{j+1} - \mathbf{p}_j \Vert}.\]

The perpendicular distance from segment \(j\) is defined as:

\[\mathbf{d}_j(t) = (\mathbf{p}(t) - \mathbf{p}_j) - ((\mathbf{p}(t) - \mathbf{p}_j)\mathbf{N}_j)\mathbf{N}_j.\]

A corridor width on the infinity norm is defined for each corridor:

\[\Vert \mathbf{d}_j(t)\Vert_\infty \le \delta_j, \quad t_j \le t \le t_{j+1}.\]

The constraint can be incorporated into the QP by introducing \(n\) intermediate points as:

\[\left\vert \mathbf{x}_W\cdot \mathbf{d}_j\left( t_j + \frac{i}{1+n}(t_{j+1} - t_j) \right)\right\vert \le \delta_j, \quad i = 1, \cdots, n.\]

Equivalently for \(\mathbf{y}_W, \mathbf{z}_W\).

Optimal segment times

The arrival times at different keyframes is important and may be specified.

Try to find a better solution by allowing more time for some segments while taking the same amount of time away from the others.

Describe a method for finding the optimal relative segment times for a given set of keyframes.

For \(T_j = t_j - t_{j-1}\), solve the minimization problem:

\[\min f(\mathbf{T})\] \[s.t.\begin{cases} \sum_{j=1}^m T_j = t_m \\ T_j \ge 0. \end{cases}\]

Where \(\mathbf{T} = [T_1,T_2,\cdots,T_m]\).

Solving the optimization problem via a constrained gradient descent method.

Computing the directional derivative by:

\[\nabla_{g_j}f = \frac{f(\mathbf{T}+h\mathbf{g}_j) - f(\mathbf{T})}{h},\]

where

  • \(h\) is some small number.
  • \(\mathbf{g}_j\) is constructed that the \(j\)th element has a value of \(1\), and all other elements have the value \(\frac{-1}{m-2}\).
    • \(\sum\mathbf{g}_j = 0\).

Circle trajectory

\[x = r\cos\theta, y = r\sin\theta.\]

Gerono lemniscate trajectory

\[x = r\cos\theta, y = r\sin\theta\cos\theta.\]

Cylindrical spiral trajectory

\[x = r\cos \theta, y = r\sin\theta, z = \pm \frac{h}{2\pi}\theta.\]

Heading trajectory

Trajectory Optimization

References

  1. https://www.quora.com/Why-do-quadrocopters-compute-minimum-snap-jounce-paths. ↩