Normalization

归一化是为了消除不同数据之间的量纲，将数据映射到指定的范围，方便数据的比较与共同处理。

  • 常见的映射范围有：\([0,1],[-1,1]\)。
  • 经过归一化处理，数据处于同一数量级，可以消除指标之间的量纲和量纲单位的影响，便于不同数据指标能够进行比较和加权。

Min-Max归一化 (线性)

  • 映射到\([0,1]\)范围。
\[x_{new} = \frac{x - x_{min}}{x_{max} - x_{min}}.\]

平均归一化 (线性)

  • 将均值为\(\mu\)的数据映射为均值为\(0\)。
  • 映射到\([-1,1]\)范围。
\[x_{new} = \frac{x - \mu}{x_{max} - x_{min}}.\]

对数函数归一化 (非线性)

  • 非线性归一化常用于数据分析比较大的场景，有些数值很大，有些很小，需要根据数据分布的情况，决定非线性函数(log、指数、正切等)的选取。
\[x_{new} = \log_{10}(x).\]

反正切函数归一化 (非线性)

  • 如果要映射到\([0,1]\)，则数据都应该大于等于\(0\)，小于\(0\)的数据将会映射到\([-1,0]\)。
\[x_{new} = \arctan(x)*2/\pi.\]

Standardization (Normalization)

标准化是为了方便数据的下一步处理而进行的数据缩放等变换，如数据经过\(0\)均值标准化后，更利于使用标准正态分布的性质进行处理；如在神经网络中，标准化不同数据的输入可以加快训练网络的收敛性。

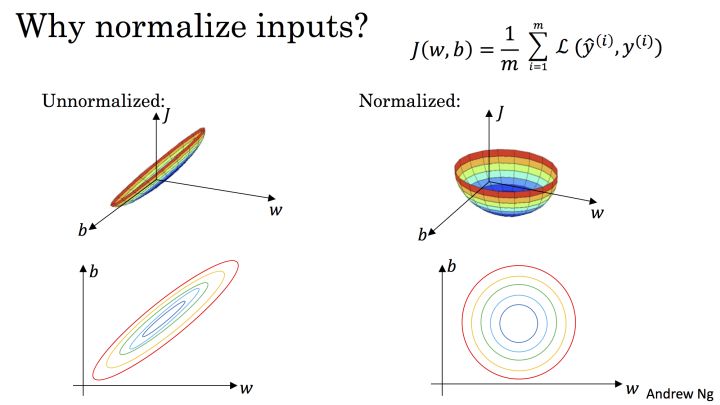
  • 标准化和归一化的定义有相似之处，但是标准化适应范围更广，被用于很多机器学习算法中(SVM、逻辑回归、NN等)。
  • 机器学习中可能会处理不同类别的数据(语音、图像等)，这些数据可能是高维的，数据标准化后会使每个特征中的数据符合正态分布。

Z-Score标准化

  • 基于正态分布的假设，将数据变换为均值为0，标准差为1的标准正态分布。
  • 即使数据不服从正态分布，也可以使用，适用于数据的最大值和最小值未知或存在孤立点。
\[x_{new} = \frac{x-\mu}{\sigma},\]

where \(\mu\) is the mean of the sampled data, \(\sigma\) is the standard deviation.

中心化

  • 映射到均值为\(0\)，对标准差无要求。
\[x_{new} = x - \mu.\]

Batch Normalization

  • Paper.
  • 利用正则化减少内部相关变量分布的偏移，提高算法鲁棒性。
  • 具有正则化的效果。
  • 提高模型的泛化能力。
  • 允许更高的学习速率，加快收敛。

算法分为两个部分：

  1. Batch Normalization Transform:

  2. Training the BN network:

Regularization

正则化是利用先验知识(启发式)，在处理过程中引入正则化因子（regulator），增加引导约束的作用，如在逻辑回归中使用正则化，可以有效降低过拟合的现象。

  • 用一组原问题相邻近的适定问题的解去逼近原问题的解。
  • 主要用于避免过拟合、减小网络误差和网络复杂度。

一般形式如下：

\[J(\theta) = \frac{1}{m} \sum_{i=1}^m L(f(x),y) + \lambda R(f).\]

其中，第一项为Loss function，第二项为正则项，\(\lambda\)为权重调整参数。

常用的正则项：

  • \(L_1\): 比\(L_2\)更易于得到稀疏解.
  • \(L_2\): 控制过拟合的效果比\(L_1\)好.
  • Dropout: 降低网络复杂度，防止过拟合.
  • Entropy: 增加探索.

\(L_p\)范数定义:

  • \(L_0\) (非零元素的个数): \(\lVert w \rVert_0 = count(x_i\neq 0)\).
  • \(L_1\) (每个元素绝对值之和): \(\lVert w \rVert_1 = \sum_{i=1}^n \vert x \vert\).
  • \(L_2\) (欧氏距离): \(\lVert w \rVert_2 = \sqrt{\sum_{i=0}^n x_i^2}\).
  • \(L_p\): \(\lVert w \rVert_p = \left( \sum_{i=1}^n x_i^p \right)^{1/p}\).
  • \(L_\infty\) (所有元素中绝对值最大的): \(\lVert w \rVert_\infty = \max_{1 \le i \le n}\vert x_i \vert\).

\(L_1\)正则

  • 在目标函数中加入惩罚所有网络参数\(\theta\)的绝对值。
    • 将导致权重参数在优化期间变稀疏，非常接近0。
  • 凸函数，不是处处可微分。
  • 得到的是稀疏解，最优解常出现于顶点上，且顶点上的\(w\)只有很少的元素为非零。
\[J(\theta) = \frac{1}{m}\sum_{i=1}^m L(\hat{y}, y) + \frac{\lambda}{m}\lVert \theta \rVert_1.\]

\(L_2\)正则

  • 在目标函数中加入惩罚所有网络参数\(\theta\)的平方。
    • 严重惩罚峰值大的权重参数，偏向于比较均匀的权重。
    • 使用\(L_2\)最终意味着每个权重参数线性衰减至0：\(\theta = \theta - \lambda\theta\)。
  • 凸函数，处处可微分。
  • 易于优化。
\[J(\theta) = \frac{1}{m}\sum_{i=1}^m L(\hat{y}, y) + \frac{\lambda}{2m}\lVert \theta \rVert_2^2.\]

最大范数正则

  • 对每一个神经元的权重参数设置绝对上限：\(\Vert\theta\Vert_2 < C\) (C的典型值约为3或4)。
  • 即使学习率设置的很高，网络也不会爆炸，因为更新是有界的。

Dropout

  • Paper.
  • 主要用于神经网络，使神经网络中的某些神经元随机失活，让模型不过度依赖某一神经元，达到增强模型鲁棒性以及控制过拟合的效果。
    • 让神经元以概率\(p\)为活动的，否则将其设置为0。

References