Motivation

Quadrotor

  • Applications: dirty, dangerous, dull tasks.
    • Search and rescue missions.
    • Various surveillance tasks.
    • Acting as mobile nodes in communication networks.
    • Quick delivery systems.
      • Medical supplies.
  • Some serious problem:
    • How to hold algorithmically driven robots responsible for devastating actions?
    • The lowered bar of entry to start warfare with cheaper robots to restrict the use of autonomous systems in warfare.
  • Control:
    • Lacking in stability compared to traditional designs.
      • With smaller units resulting in lower inertia moments being more susceptible to complex aerodynamical effects.
    • Require intricate control design in order to guarantee stable flight.
      • Requirement on computational speed and accuracy.
        • The dynamics are quick and non-linear.
    • Control schemes:
      • Hierarchical:
        • Lower level controllers:
          • control of electrical signals to rotors.
          • attitude controller.
          • positional and altitude controller.
        • Higher level controllers:
          • path planning.
          • problem solving.
          • cooperation between humans or other units.
    • Related works:
      • PID.
      • LQR.
      • \(H_\infty\).
      • Sliding mode.
      • MPC.
      • RL:
        • Attitude control.
        • Positional control.
        • S2R problem:
          • Not transfer to real hardware and test on notably different simulated setups.
          • Transferring successfully to real hardware but noticing some performance degradation.
          • Implement methods of handling the S2R-gap and seeing improved transfer results.
          • None of these methods implemented the robust wersions of the underlying RL formulation.

S2R Transfer

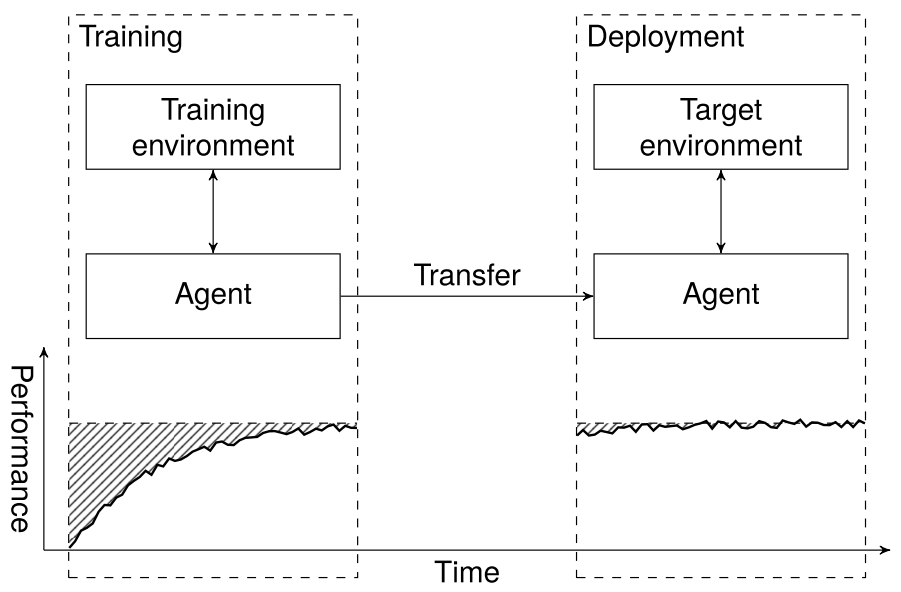
  • Sim-to-Reality (S2R) transfer in RL is a promising approach of solving costly exploration in real systems.
    • Modifying the training such that safety guarantees on the training policy.
      • Safe RL.
      • Modify the objective function or exploration policy are studied to minimize the risk costly exploration.
    • Improving the transferability of simulator-trained policies to actual systems.
      • Transfer Learning in RL.
      • The agents performance on environments different than the environment trained in.
  • Problem:
    • S2R solves the costly exploration problem, but introduces robustness and generalization concerns.
    • The generalization of transferring policies from simulators to real systems.
    • Even if the agent finds an optimal policy inside the simulated environment, it is difficult to guarantee anything about the performance on the target environments.
  • Related works:
    • Making the S2R gap smaller:
      • Making the simulated environment behave more closely to the target environment.
      • Accurate parameter estimation and more precise system indentification.
      • Combine rollouts in real environment and using the trajectories as feedback to improve the model behavior.
      • Drawbacks:
        • The assumption is that there exists only one single target environment, but there may be multiple possible target environments.
        • It is difficult or costly to gather information from the target environments.
    • Consider random environments:
      • Training on several model dynamics sampled from a priori parameter distribution representing the agents, which have been shown to better generalize to real systems.
      • Drawbacks:
        • The exact dynamics of the target environments is difficult to emulate.
    • Robust control:
      • Design controller to tolerant to misspecifications between models and real systems.
      • The controlled system in robust control is assumed to be unknown but bounded.
      • The most popular robust controller designs is the \(H_\infty\) controller.
        • Work with the average bounded system optimizes instead for the worst-case system.
        • Guarantee stability for all systems inside the bounds.
        • Thus, it is popular for situation where robustness is required.
  • Ideas:
    • Robust MDP.
    • RL + Robust Control.
    • Create agents with embedded uncertainty about the simulated environment.
    • Training the agent in a simple environment and test on versions of the simulator with different environment parameters.
      • Training environment.
      • Target environments.
  • Results:
    • Agents with higher level of robustness outperformed the standard agents in these environments.
    • The added robustness increases generality and can help when transferring policies from simulators to reality.

Method

  • Goal: Formulate a training method for RL agents to bridge the S2R gap.
  • Robust MDP:
    • Uncertainty sets can be expressed in state space instead of probability distributions over the state space.

Framework

Model Uncertainty

  • Express the uncertainty of the transition model through some uncertainty set in which all the possible transition models lie.

Inner Problem Definition

For discrete state space:

  • The transition model can be expressed as a set of transition matrices consisting of finitely many elements of transition probabilities from and to each state given an action.
  • Define the inner problem as:
\[\min_{p\in P} \mathbb{E}_p[V^\pi(s_{s+1})] = \min_{p \in P}\sum_{i=1}^{\vert S \vert} p(s_i\vert s_t,a_t) V^\pi(s_i).\]

For continuous state space:

  • Remove the enumerability of the states.
  • The inner problem can be transformed into:
\[\min_{p\in P} \mathbb{E}_p[V^\pi(s_{s+1})] = \min_{p\in P}\int_S p(s\vert s_t,a_t)V^\pi(s)ds.\]

The above inner problem expectation calculation is difficult to evaluate, since \(V^\pi\) in this setting will be a highly non-linear structure.

Then, make a huge simplifying assumption to this problem:

  • In deterministic environments, the transition distributions \(P\) degenerate the expectation evaluation becomes trivial.
  • Let \(P^U\) be a set of transition models with degenerate distributions \(p^u\) parameterized by states \(u\).
  • Then, all probability density is located at \(u\).
\[\min_{p^u\in P^U} \mathbb{E}_{p^u}[V^\pi(s_{s+1})] = \min_{p^u\in P^U}\int_S p^u(s\vert s_t,a_t)V^\pi(s)ds = \min_{p^u\in P^U} V^\pi(u).\]

Uncertainty Set

  • View the uncertainty set as a possibility to handle unmodelled behaviors (which are difficult to quantify).
    • Wind.
    • Consider the sum of all of the unmodelled dynamics as some noise added to the transition dynamics.
  • Reasons:
    • The parameters of the system are not estimated.
    • The model is crude and a lot of uncertainty would probably come from unmodelled dynamics.
    • The uncertainty modeling becomes simpler to implement.

The deterministic model can be seen as a degenerate distribution:

  • Parameterized by the point in state space.
  • The entirely of the probability density is located.
  • The uncertainty set can be reinterpreted as a set over the state space instead over transition dynamics.

Consider an uncertainty set around each observed state \(s\) in a trajectory:

\[S_U(s) = \{ s+u\vert \forall u \in U(s) \},\]

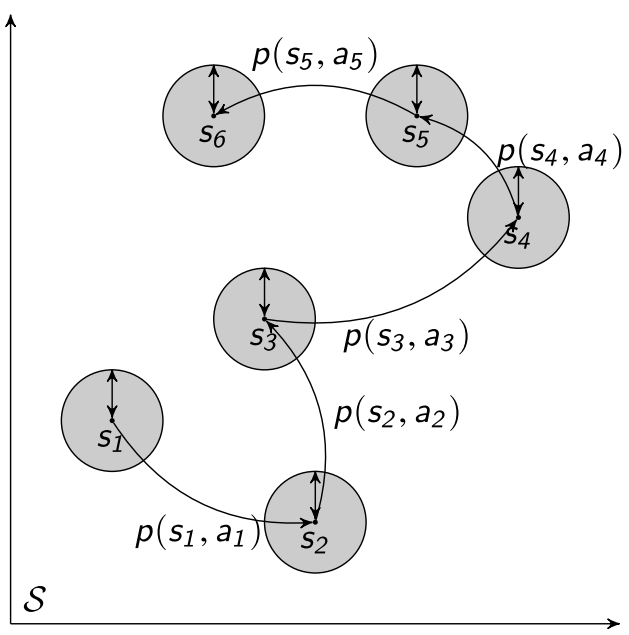
where \(U(s)\) is a priori asserted uncertainty set.

Let \(U(s)\) as \(L_2\) spheres in the state space:

\[U_\rho(s) = \{ u\in \mathbb{R}^S \vert \lVert u \rVert_2 < \rho \},\]

where \(\rho\) is the size of uncertainty, can be viewed as radius.

Solving Inner Problem

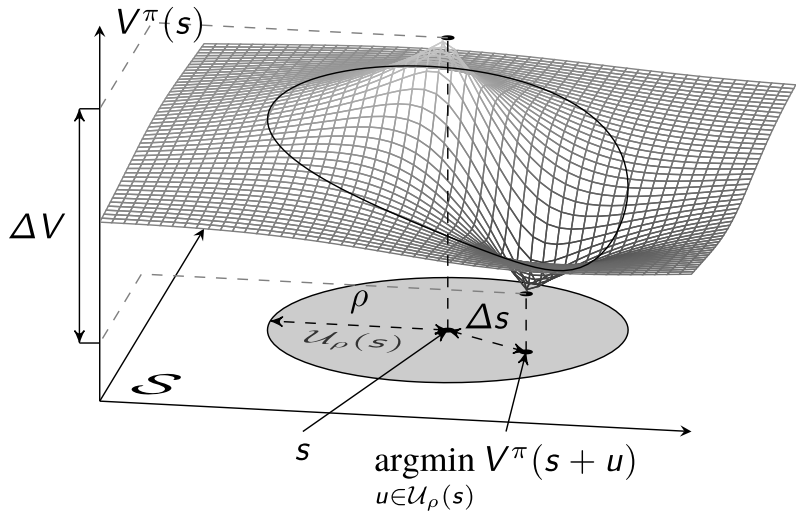
Minimize the value function given the uncertainty set:

\[\min_{u\in U}V_\phi^\pi(s+u).\]

Algorithm:

  • Hyperparameters:
    • \(k\) for width, controls how many points are computed in parallel.
    • \(n\) for depth.
    • \(n\) controls how many gradient steps are taken before we assume convergence.

Robust PPO

  • Replace training targets using Bellman equations with the robust Bellman equations instead.

Estimate \(\hat{R}\) and \(\hat{A}\)

  • Using truncated \(n\)-step TD to estimate.
  • Apply a decaying scheme for parameter \(\lambda\).
    • In order to reduce computations, handle episodic tasks, reduce reliance on too long traces.

Define the \(n\)-step robust returns for a trajectory:

\[\begin{aligned} \hat{R}_t^{\rho(1)} & = r_t + \gamma \min_{u\in U_\rho}V^\pi(s_{t+1} + u), \\ \hat{R}_t^{\rho(2)} & = r_t + \gamma r_{t+1} + \gamma^2 \min_{u\in U_\rho}V^\pi(s_{t+2} + u), \\ & \vdots \\ \hat{R}_t^{\rho(n)} & = \sum_{k=0}^{n-1}\gamma^k r_{t+k} + \gamma^n \min_{u\in U_\rho}V^\pi(s_{t+n} + u). \end{aligned}\]

Define the \(n\)-step robust advantage estimates:

\[\hat{A}_t^{\rho(n)} = \hat{R}_t^{\rho(n)} - V^\pi(s_t).\]

Using Truncated TD(\(\lambda\)) to estimate \(\hat{R}_t\):

\[\begin{aligned} \hat{R}_t^{\rho TTD(\lambda,N)} & = (1-\lambda)\hat{R}_t^{\rho(1)} + \lambda\left( (1-\lambda)\hat{R}_t^{\rho(2)} + \lambda(\cdots) \right) \\ & = (1-\lambda)\sum_{n=1}^{N-1}\lambda^{n-1}\hat{R}_t^{\rho(n)} + \lambda^{N-1}\hat{R}_t^{\rho(N)}. \end{aligned}\]

Using Truncated GAE(\(\lambda\)) to estimate \(\hat{A}_t\):

\[\hat{A}_t^{\rho TGAE(\lambda,N)} = (1-\lambda)\sum_{n=1}^{N-1}\lambda^{n-1}\hat{A}_t^{\rho(n)} + \lambda^{N-1}\hat{A}_t^{\rho(N)}.\]

Algorithm:

Algorithm of Robust PPO

  • Incorporate a decaying scheme for the trace parameter \(\lambda\):
    • High \(\lambda\) greatly improves training in early iterations when the critic network has not yet converged to a useful approximator.
    • \(\lambda=0\) is needed in order to represent the correct robust equations for training targets.
    • Using a linear decaying scheme, \(\lambda_{decay}\) controls the speed at which the trace reaches zero.

Robust TD-error to fit the value function approximator:

\[\phi_{k+1} = \arg\min_\phi\frac{1}{\vert B\vert T}\sum_{\tau\in B}\sum_{t=0}^T\left( V_\phi(s_t) - \hat{R}_t^{\rho TTD(\lambda,N)} \right)^2.\]

Robust advantage estimation to fit the policy function:

\[\theta_{k+1} = \arg\max_\theta J^{PPO}(\theta\vert \hat{A}_t^{\rho TGAE(\lambda,N)}).\]

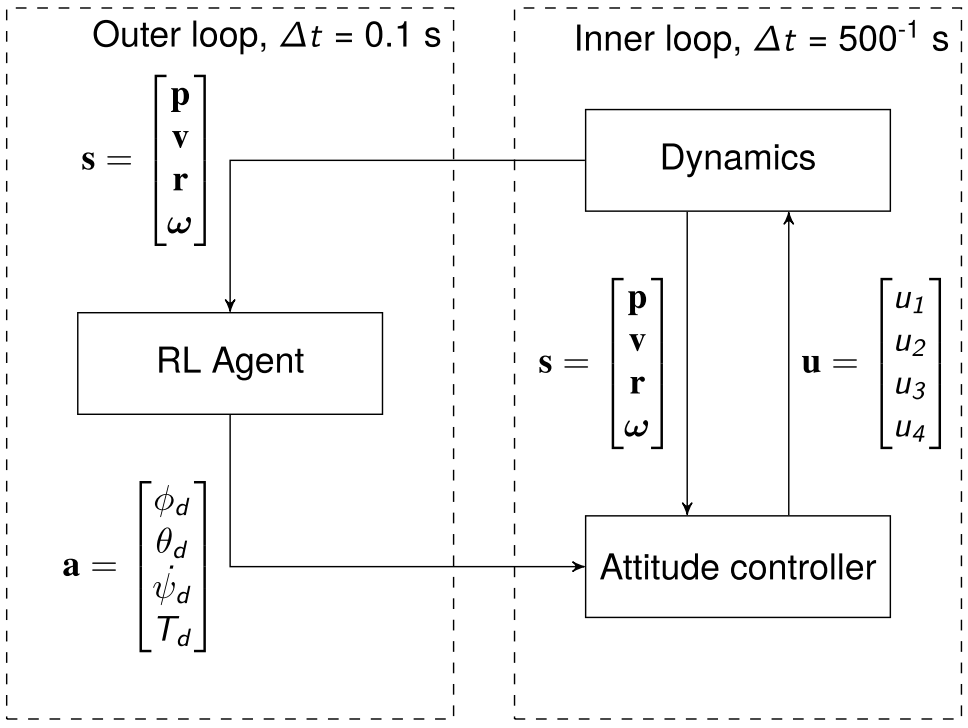
Robust PPO for UAV positional control

State Input

\[(p_t^e, v, \Theta, \omega, e_{p_t}, e_{v_t}, e_{\sigma_t}).\]
  • \(p_t^e = p_t^g - p_t\).

Action Output

\[(\phi_d,\theta_d,\dot{\psi}_d, T_d).\]
  • Remove yaw rate, set it to a constant \(\dot{\psi}_d = 0\).
  • Rescale the possible range for the remaining action outputs:
    • Angles \(\phi_d, \theta_d\) range: \([-10^\circ,10^\circ]\).
    • Thrust \(T_d\) range: \([10000,65535]\).
  • Normalize the action: \([-1,1]\).

Environment terminal time

  • The agent is more interested in the behavior before reaching the goal position.
  • Then, episode is needed.
  • Add a time limit \(T_{limit}\).
    • In order to let the agent see initial states more often.
  • End the episode when:
    • A failure state.
      • \(V(s_T) = -1\).
    • Maximum number of interactions has been reached (limit time).
      • \(V(s_T) = V(s_T)\).

Neural Networks

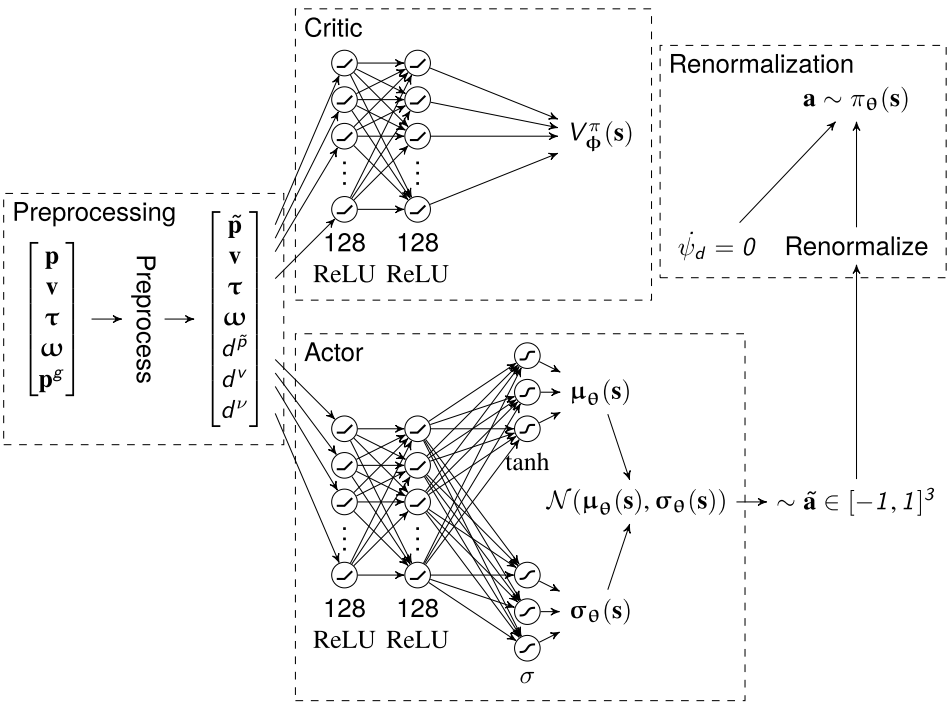
  • MLP.
  • Critic network:
    • The output layer is a simple linear layer with one output.
  • Actor network:
    • Two output layers representing parameters for Gaussian distributions:
      • Mean values \(\mu_\theta(s)\in [-1,1]\) with tanh activation function.
      • Standard deviations \(\sigma_\theta(s)\in[0,1]\) with sigmoid activation function, in order to impose limits on the variance of the distribution.

Regularization

Definition:

  • Regularization is a general term for modification to objective functions to guide optimization in ill-posed problem.
  • In ML, it is widely used to combat overfitting.

Formulate the regularization to objective function as:

\[J(\theta) + \sum_{i=1}^I \beta_i l_i(\theta),\]

where \(\beta_i\) is the regularization weight to set the strength of the regularization term.

Using regularization in robust PPO:

  • Entropy regularization for actor network.
    • Trade-off between exploration and exploitation.
      • Exploitation: using current knowledge to collect high rewards.
      • Exploration: searching the policy space to potentially find better policies to follow.
    • Usually resolved with heuristical methods.
    • Entropy can be seen as the uncertainty of a distribution.
      • \(H(p) = -\int_X p(x)\log(x)dx\).
    • Entropy regularization: \(l_H(\theta) = \mathbb{E}_{\pi_\theta}[H(\pi_\theta(a_t\vert s_t))]\).
      • Prevent too deterministic policies.
      • Encourage a higher level of exploration in the on-policy setting.
  • \(L_1\) regularization for both actor and critic networks.
    • Tend to favor sparsity in the weight vector.
    • Reduce the model complexity.
      • Tend towards simpler models by pruning model weights.
      • Does not impact the original objective significantly enough.
    • Parameter weights regularization:
      • For actor network weights: \(l_{L_1}(\theta) = \lVert \theta \rVert_1\).
      • For critic network weights: \(l_{L_1}(\phi) = \lVert \phi \rVert_1\).

Simulation

Implementation

  • Simulator: RLlib framework.
    • Distribute training across multiple processes.
    • Parallelize the agent rollouts.
  • Wrapper: OpenAI Gym API.
  • NNs: Pytorch.
  • Gradient method: Adam.

Training

  • Training multiple agents with values of robust radius \(\rho\in[0.001,1]\).
  • Compare these agents to the baseline of a regular PPO agent with \(\rho=0\).

Evaluation

  • Test the robustness of the policy in target environments.
    • Different to the training environment.
  • Target environments:
    • Different quadrotor mass: \(\Delta m\in [0.7,1.3]\).
    • Different motor coefficients:
      • Change the coefficients of one of the motors in the model, corresponding to damaged or worn.
      • The motors are modeled with a set of polynomial coefficients mapping digital driver values to physical values \([c_T,b_T,a_T,b_\omega,a_\omega,b_\psi,a_\psi]\).
      • Multiply these coefficients by a factor: \(\Delta \lambda \in [0.3,1]\).
    • Different PID tuning:
      • PID parameters of internal attitude controller.
      • Multiply a factor \(\Delta K_p\in[0.1,1.9]\) to the proportional gain \(K_p\) of the roll and pitch controllers: \([PID_\phi.K_p, PID_\theta.K_p, PID_{\dot{\phi}}.K_p, PID_{\dot{\theta}}.K_p]\).
  • Performance metric:
    • Use the episodic average step reward measured from an episode: \(\bar{r}(\tau) = \frac{\sum_{k=0}^{T-1}r_t}{T}\).
  • Robust performance:
    • Remove the stochastisity in the policy, picking the mean value \(\mu_\theta\) of the policy distribution.

Results

  • Convergence seems clear for agents with lower values of \(\rho\), but asymptotic performance does taper off as the radius grows.
    • Performance dropping after \(\rho = 0.1\).
  • Robustness of the agents:
    • Running each agent in different target environments.
    • The robust agents outperforms the nominal in the more extreme environment differences.
    • The robust agents do not suffer from an immediate performance drop in the nominal environment.
    • More robust agents performs similar to slightly better than the non-robust agent for environments close to the nominal.
    • Reduce the oscillations and static errors.
  • Static errors:
    • especially in the \(z\)-axis.
    • Static errors are widely understood in the control theory where controllers with integral action.
      • Integral action is the most non-Markovian part of controllers.

Future Work

  • Robust MDP for continuous control
    • Deterministic systems.
      • Moving all the uncertainty into the second order uncertainty sets (on state observations).
    • Non-deterministic systems.
      • Require measurements on probability distributions.
    • Consider other uncertainty sets on state observations.
  • Robustness of other RL algorithms
    • DQN
    • DDPG
    • SAC
  • RL for UAV control
    • End-to-end control.
    • Static errors.
      • Handle via integral action.
      • Extend the state space to include the sum of error signals.
        • Increase the dimensionality of the state space and the search space for policies.

References

  • L. Bjarre, “Robust Reinforcement Learning for Quadcopter Control,” 2019.