Nonlinear H-infinity Control for a Quadrotor
Motivation
Problem
- UAV is underactuated mechanical system, which complicate the control design stage even more.
- UAV has a high nonliear and time-varying behavior.
- It is constantly affected by aerodynamic disturbances.
- Usually models subject to unmodelled dynamics and parametric uncertainties.
Solution
- An advanced control strategy is required to achieve good performance in autonomous flight.
- With high maneuverability and robustness w.r.t.
external disturbances.
- With high maneuverability and robustness w.r.t.
- Nonlinear modelling techniques and modern nonlinear control theory are usually employed to achieve autonomous flight with high performance.
- A good choice to reject these disturbances is the nonlinear H\(_\infty\) control theory.
- Need to solve two Hamilton-Jacobi-Bellman-Isaacs partial differential equations (HJBI PDEs).
- Replace the RIccati equations in the linear H\(_\infty\) control formulation.
- But, the main problem is
the absence of a general method to solve these equations.
Strongly model-dependent.
- Need to solve two Hamilton-Jacobi-Bellman-Isaacs partial differential equations (HJBI PDEs).
Contributions
- Present an
integral predictiveandnonlinear robust controlstrategy to solve thepath followingproblem for a quadrotor. Hierarchicalcontrol structure:- A Model Predictive Controller (MPC) to track the reference trajectory.
- Consider the integral of the position error.
- A nonlinear H\(_\infty\) controller to stabilize the rotational movements.
- Consider the integral of the error.
- Cope with unknown disturbances.
- A Model Predictive Controller (MPC) to track the reference trajectory.
- Achieve a
null steady-state errorwhen sustained disturbances on the system. Parametric and structural uncertaintiesare presented to corroborate the effectivemess androbustnessof the control strategy.
Method
System Modelling
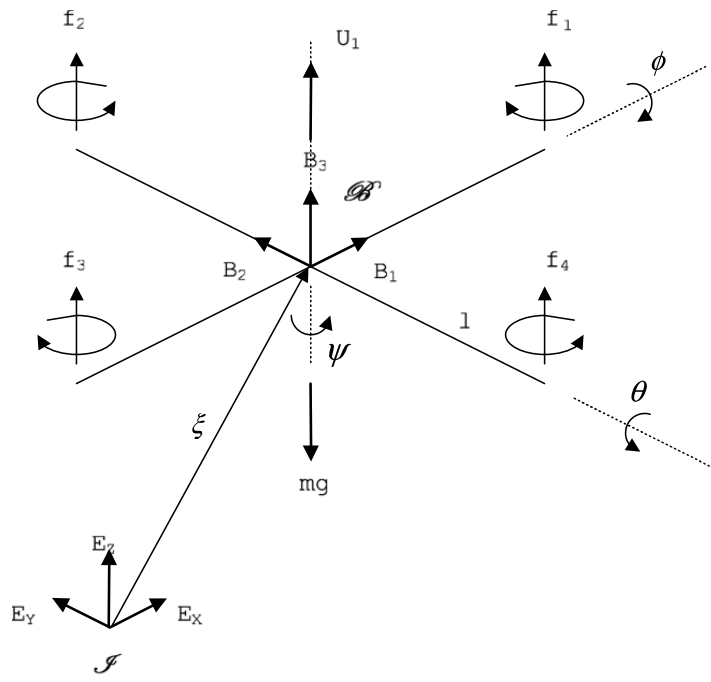
- Body frame: \(B=\{B_1,B_2,B_3\}\).
- World frame: \(E = \{E_x,E_y,E_z\}\).
- Position \(p = [x,y,z]\).
- Rotation matrix: \(R\).
- Eulers: \(\eta\).
- Roll: \(\phi\in(-\pi/2 < \phi < \pi/2)\).
- Pitch: \(\theta\in(-\pi/2 < \theta < \pi/2)\).
- Yaw: \(\psi\in(-\pi,\pi)\).
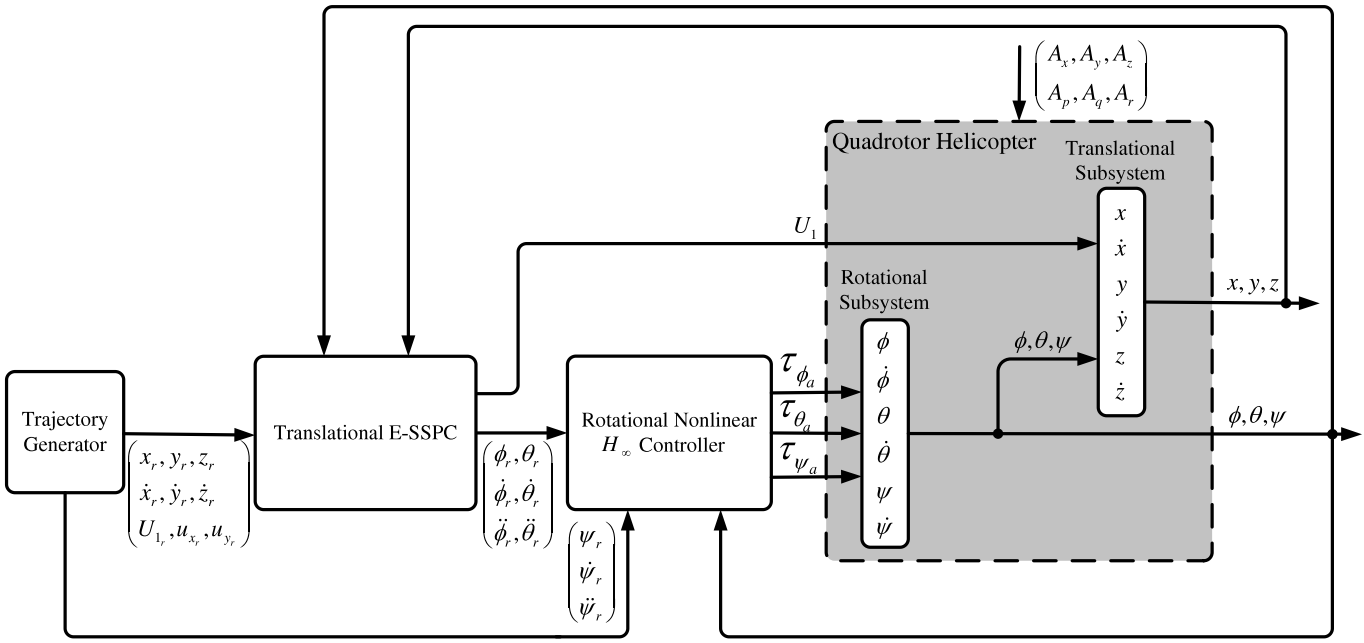
Controller
Goal: Control the quadrotor in presence of sustained external disturbances, parametric uncertainties and unmodelled dynamics.
Control strategy:
- The
reference trajectoryis provided off-line by the Trajectory Generator block.- Translational movements: \([x_r,y_r,z_r]\).
- Yaw angle is defined separately.
- Reference control inputs: \([U_{1_r}, u_{x_r}, u_{y_r}]\).
- There are no external disturbances.
- Outer Loop: translational movements.
- State-space predictive controller based on the error model (E-SSPC).
- Include the integral of the position error.
- Achieve null steady-state error.
- Height \(z\) control: total thrust \(U_1\).
- Pitch and roll control.
- Inner Loop: rotational subsystem.
- Nonlinear H\(_\infty\) controller.
- Control the angle and angle velocities.
- Using torques \(\tau\).
- Include the integral of the angle error.
- Achieve null steady-state error.
Nonlinear H\(_\infty\) Controller for attitude
Define the dynamic equation of a nonlinear system with unknown disturbance as:
where
- \(u\) is the vector of control inputs.
- \(d\) is the vector of external diaturbances.
- \(x\) is the vector of states.
Define the performance using the cost variable \(\zeta\):
where
- \(h(x)\) represents a function of the vector of states to be controlled.
- \(W\) is a weight matrix.
The optimal H\(_\infty\) problem can be posed as follows:
- Find the smallest value \(\gamma^*\ge 0\), such that for any \(\gamma\ge \gamma^*\), there exists a state feedback \(u=u(x,t)\), such that the \(L_2\) gain from \(d\) to \(\zeta\) is less than or equal to \(\gamma\):
where \(\lVert\zeta\rVert_2^2 = \zeta'\zeta = \begin{bmatrix} h'(x) & u' \end{bmatrix}W'W\begin{bmatrix} h(x) \\ u \end{bmatrix}\).
\[W'W = \begin{bmatrix} Q & S \\ s' & R \end{bmatrix},\]where
- \(Q,R\) are symmetric positive definite, and \(W'W > O\).
- \(Q - SR^{-1}S' > O\).
The optimal control signal \(u*(x,t)\) may be computed if there is a smooth solution \(V(x,t)\) to HJBI equation:
\[\frac{\partial V}{\partial t} + \frac{\partial'V}{\partial x}f(x,t) + \frac{1}{2} \frac{\partial'V}{\partial x} \left[ \frac{1}{\gamma^2}k(x,t)k'(x,t) - g(x,t)R^{-1}g'(x,t) \right]\frac{\partial V}{\partial x} - \frac{\partial'V}{\partial x}g(x,t)R^{-1}S'h(x) + \frac{1}{2}h'(x)(Q-SR^{-1}S')h(x) = 0.\]Then, the optimal state feedback control law is derived as:
For quadrotor system, define the tracking error vector as:
E-SSPC for position
- Two predictive controllers:
- Control the height through the input \(U_1\).
- Control \(x\) and \(y\) motions.
Define the state space as:
\[\dot{p}(t) = f(p(t),u_p(t)).\]References
- G. V. Raffo, M. G. Ortega, and F. R. Rubio, “An integral predictive/nonlinear H\(_\infty\) control structure for a quadrotor helicopter,” Automatica, vol. 46, no. 1, pp. 29–39, Jan. 2010.