Definition

\(L^p\)空间是由\(p\)次可积函数组成的空间，对应\(l^p\)可数维度空间是由\(p\)次可和序列组成的空间，叫勒贝格空间（Henri Léon Lebesgue）。

\(L^p\)空间

当空间维度无穷且不可数时，无法运用有限维或可数维度空间来定义范数，此时考虑所有绝对值的\(p\)次幂在\(s\)可积的函数：

\[L^p(S,\mu) = \left\{ f;\Vert f\Vert_p = \left( \int_S \vert f \vert^p d\mu \right)^{\frac{1}{p}} < \infty \right\}.\]

\(l^p\)空间

当空间维数无限可数时，定义\(p\)-范数如下：

\[\Vert (x_n)_{n\in N}\Vert_p = \left(\vert x_1\vert^p + \vert x_2\vert^p + \cdots + \vert x_n\vert^p + \vert x_{n+1}\vert^p + \cdots \right)^{\frac{1}{p}} = \left( \sum_{n=1}^N \vert x_n\vert^p \right)^{\frac{1}{p}}.\]

其中，

  • \(l^1\)空间：所有绝对收敛级数列构成的空间。
  • \(l^2\)空间：所有平方收敛级数列构成的空间。
  • \(l^\infty\)空间：所有有界数列构成的空间。

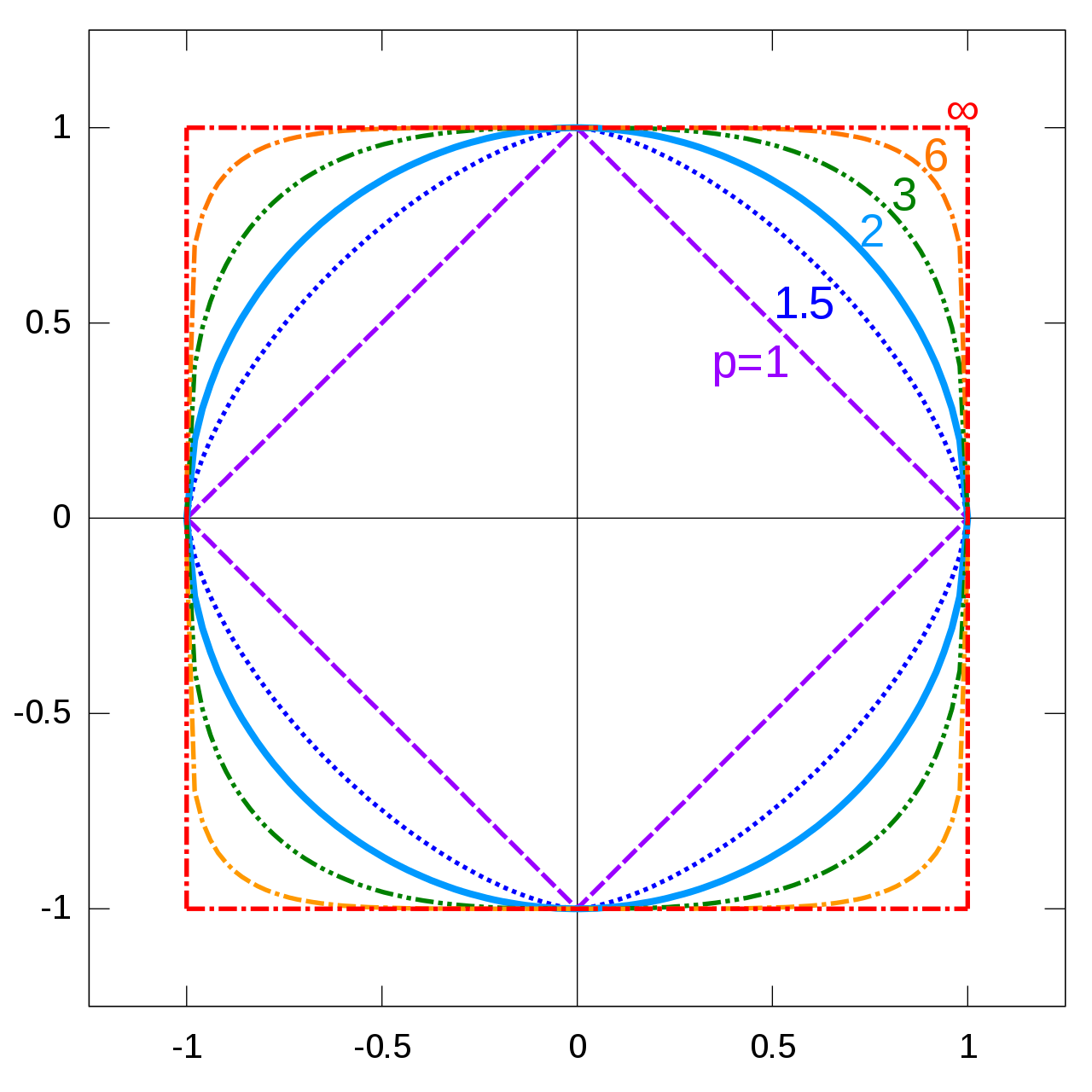
Norm

具有长度概念的函数，拥有范数的向量空间为赋范向量空间。

  • 向量范数：表征向量空间中向量的大小。
  • 矩阵范数：表征两个向量之间变化的大小。

Vector Norm

\(l^0\) Norm

  • 用于度量向量中非零元素的个数。
\[\Vert \mathbf{x}\Vert_0 = count(i\vert x_i \neq 0).\]

\(l^1\) Norm

  • 每个元素绝对值之和。
  • 曼哈顿距离。
  • 绝对误差和。
  • 稀疏规则算子，通过\(l^1\)范数可以实现特征的稀疏，去掉一些没信息的特征。
    • 如：在对用户的电影爱好做分类时，用户有100个特征，可能只有十几个特征是对分类有用的，大部分特征如身高、体重等可能都是无用的，利用\(l^1\)范数就可以过滤掉无用的特征信息。
\[\Vert \mathbf{x}\Vert_1 = \sum_{i=1}^N\vert x_i\vert.\]

\(l^2\) Norm

  • 向量元素的平方和再开方。
  • 欧几里得距离。
  • 平方差和。
  • 常用于优化目标函数的正则化项，防止模型为了迎合训练集而导致的过拟合现象，提高模型的泛化能力。
\[\Vert \mathbf{x}\Vert_2 = \sqrt{\sum_{i=1}^N x_i^2}.\]

\(l^\infty\) Norm

  • 所有元素绝对值中的最大值。
\[\Vert \mathbf{x}\Vert_\infty = \max_{1\le i \le N}\vert x_i\vert.\]

\(l^{-\infty}\) Norm

  • 所有元素绝对值中的最小值。
\[\Vert \mathbf{x}\Vert_{-\infty} = \min_{1\le i \le N}\vert x_i\vert.\]

Matrix Norm

\(l^1\) Norm

  • 列和范数。
  • 矩阵所有列向量绝对值之和的最大值。
\[\Vert \mathbf{A}\Vert_1 = \max_j \sum_{i=1}^m \vert a_{ij}\vert.\]

\(l^2\) Norm

  • 谱范数。
  • 矩阵\(A^T A\)的最大特征值的开方。
\[\Vert \mathbf{A}\Vert_2 = \sqrt{\lambda}.\]

\(l^\infty\) Norm

  • 行和范数。
  • 矩阵所有行向量绝对值之和的最大值。
\[\Vert \mathbf{A}\Vert_\infty = \max_i \sum_{j=1}^n \vert a_{ij}\vert.\]

\(l^F\) Norm

  • Frobenius范数。
  • 矩阵元素绝对值的平方和再开方。
\[\Vert \mathbf{A}\Vert_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n \vert a_{ij}\vert^2}.\]

Nuclear Norm

  • 核范数。
  • 矩阵的奇异值之和。
\[\Vert \mathbf{A}\Vert_* = \sum_{i=1}^n \lambda_i.\]