Jensen's Inequality
Definition
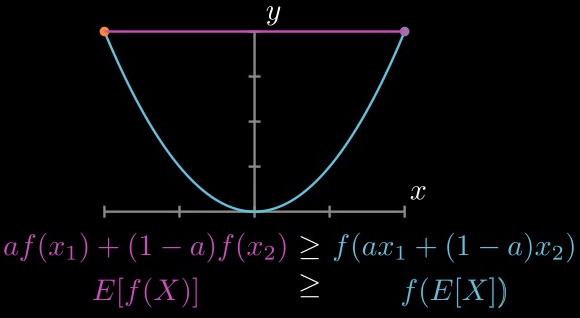
For any convex function \(f(x)\), we have:
Example
The variance of every random variable \(X\) is a positive value, i.e.:
\[Var(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 \ge 0.\]Then,
\[\mathbb{E}[X^2]\ge (\mathbb{E}[X])^2.\]Define \(f(x) = x^2\) (convex function), thus:
\[\mathbb{E}[f(X)]\ge f(\mathbb{E}[X]).\]Convex Function
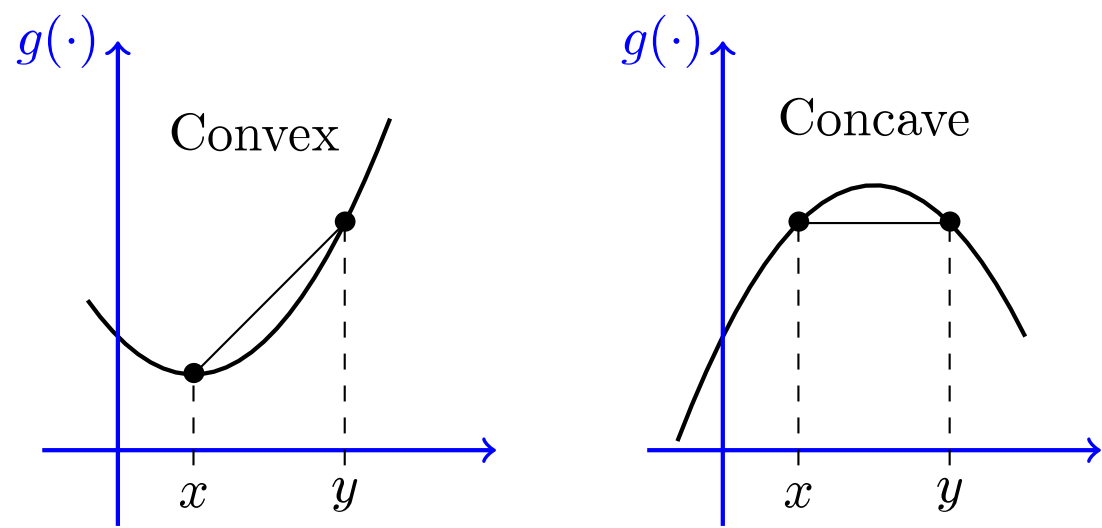
Consider a function \(g: I\to \mathbb{R}\):
- Convex: \(g(\alpha x + (1-\alpha)y) \le \alpha g(x) + (1-\alpha)g(y), \forall \alpha\in[0,1]\).
- Concave: \(g(\alpha x + (1-\alpha)y) \ge \alpha g(x) + (1-\alpha)g(y), \forall \alpha\in[0,1]\).