KL, JS Divergence and Wasserstein Distance
KL (Kullback-Leibler) Divergence
KL散度又称相对熵,为信息散度(增益),是两个概率分布\(P\)和\(Q\)之间差别的非对称的度量,即度量使用基于\(Q\)的编码方式对\(P\)进行编码所需的额外bits数,\(P\)表示数据的真实分布,则\(Q\)表示\(P\)的近似分布。
\[D_{KL}(P \Vert Q) = - \sum_{x \in X} P(x) \log \frac{1}{P(x)} + \sum_{x \in X} P(x) \log \frac{1}{Q(x)} = \sum_{x \in X} P(x) \log \frac{P(x)}{Q(x)}.\]KL散度性质:
- 不对称性;
- 为非负值,因为对数函数为凸函数;
- 不满足三角不等式。
KL散度局限性:
当两个分布距离很远,完全没有重叠时,KL散度值失去意义。
单变量高斯分布概率密度:
\[N(x\vert \mu,\sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}}\exp\left\{ - \frac{1}{2\sigma^2}(x - \mu)^2 \right\}.\]多变量高斯分布概率密度,其中\(\Sigma\)为协方差矩阵:
\[N(x\vert \mu,\Sigma) = \frac{1}{(2\pi)^{n/2} \lvert \Sigma \rvert^{1/2}}\exp\left\{ -\frac{1}{2}(x - \mu)^T \Sigma^{-1}(x-\mu) \right\}.\]矩阵的迹的性质:
- \(tr(\alpha A + \beta B) = \alpha tr(A) + \beta tr(B)\).
- \(tr(A) = tr(A^T)\).
- \(tr(AB) = tr(BA)\).
- \(tr(ABC) = tr(CAB) = tr(BCA)\).
- \(\lambda^T A \lambda = tr(\lambda^T A \lambda) = tr(A \lambda \lambda^T)\).
多变量分布中期望与协方差的性质:
\[\mathbb{E}[xx^T] = \Sigma + \mu\mu^T.\] \[\begin{aligned} \Sigma & = \mathbb{E}\left[ (x-\mu)(x- \mu)^T \right] \\ & = \mathbb{E}[xx^T - x\mu^T - \mu x^T + \mu\mu^T] \\ & = \mathbb{E}[xx^T] - \mu\mu^T. \end{aligned}\] \[\begin{aligned} \mathbb{E}(x^T A x) & = \mathbb{E}[tr(x^T A x)] \\ & = \mathbb{E}{tr(Axx^T)} \\ & = tr[\mathbb{E}(Axx^T)] \\ & = tr[A\mathbb{E}(xx^T)] \\ & = tr[A(\Sigma + \mu\mu^T)] \\ & = tr(A\Sigma) + tr(A\mu\mu^T) \\ & = tr(A\Sigma)+ tr(\mu^T A \mu) \\ & = tr(A\Sigma) + \mu^T A \mu. \end{aligned}\]在强化学习策略比较中:
Define the policies as multivariate Gaussian distribution:
where
- \(\mu_1,\mu_2\) are produced by the neural networks \(\pi_{\theta_1}(s), \pi_{\theta_2}(s)\).
- \(\Sigma = \Sigma_1 = \Sigma_2\) is a
diagonal matrixindependent of state \(s\).
Then,
\[\begin{aligned} D_{KL}(\pi_1 \Vert \pi_2) & = \mathbb{E}_{\pi_1}[\log \pi_1 - \log \pi_2] \\ & = \frac{1}{2}\mathbb{E}_{\pi_1}\left[ -\log\lvert\Sigma_1 \rvert - (x - \mu_1)^T \Sigma_1^{-1}(x - \mu_1) + \log\lvert\Sigma_2 \rvert + (x - \mu_2)^T \Sigma_2^{-1}(x - \mu_2) \right] \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} + \frac{1}{2}\mathbb{E}_{\pi_1}\left[ - (x - \mu_1)^T \Sigma_1^{-1}(x - \mu_1) + (x - \mu_2)^T \Sigma_2^{-1}(x - \mu_2) \right] \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} + \frac{1}{2}\mathbb{E}_{\pi_1}\left\{ -tr\left[ \Sigma_1^{-1} (x - \mu_1) (x - \mu_1)^T \right] + tr\left[ \Sigma_2^{-1} (x - \mu_2) (x - \mu_2)^T \right] \right\} \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} + \frac{1}{2}\mathbb{E}_{\pi_1}\left\{ -tr\left[ \Sigma_1^{-1} (x - \mu_1) (x - \mu_1)^T \right] \right\} + \frac{1}{2}\mathbb{E}_{\pi_1}\left\{ tr\left[ \Sigma_2^{-1} (x - \mu_2) (x - \mu_2)^T \right] \right\} \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - \frac{1}{2} tr \left\{ \mathbb{E}_{\pi_1}\left[ \Sigma_1^{-1} (x - \mu_1) (x - \mu_1)^T \right] \right\} + \frac{1}{2} tr \left\{ \mathbb{E}_{\pi_1}\left[ \Sigma_2^{-1} (x - \mu_2) (x - \mu_2)^T \right] \right\} \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - \frac{1}{2} tr \left\{ \Sigma_1^{-1} \mathbb{E}_{\pi_1}\left[ (x - \mu_1) (x - \mu_1)^T \right] \right\} + \frac{1}{2} tr \left\{ \mathbb{E}_{\pi_1}\left[ \Sigma_2^{-1} (xx^T - \mu_2 x^T - x\mu_2^T + \mu_2 \mu_2^T) \right] \right\} \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - \frac{1}{2} tr \left\{ \Sigma_1^{-1} \Sigma_1 \right\} + \frac{1}{2} tr \left\{ \Sigma_2^{-1} \mathbb{E}_{\pi_1}\left[ xx^T - \mu_2 x^T - x\mu_2^T + \mu_2 \mu_2^T \right] \right\} \\ & = \frac{1}{2}\log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - \frac{1}{2} tr \left\{ \Sigma_1^{-1} \Sigma_1 \right\} + \frac{1}{2} tr \left\{ \Sigma_2^{-1} \left[ \Sigma_1 + \mu_1 \mu_1^T - \mu_2 \mu_1^T - \mu_1 \mu_2^T + \mu_2 \mu_2^T \right] \right\} \\ & = \frac{1}{2} \left\{ \log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - tr \left\{ \Sigma_1^{-1} \Sigma_1 \right\} + tr(\Sigma_2^{-1}\Sigma_1) + tr \left\{ \Sigma_2^{-1} \left[ \mu_1 \mu_1^T - \mu_2 \mu_1^T - \mu_1 \mu_2^T + \mu_2 \mu_2^T \right] \right\} \right\} \\ & = \frac{1}{2} \left\{ \log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - tr \left\{ \Sigma_1^{-1} \Sigma_1 \right\} + tr(\Sigma_2^{-1}\Sigma_1) + tr \left\{ \Sigma_2^{-1} \mu_1 \mu_1^T - \Sigma_2^{-1}\mu_2 \mu_1^T - \Sigma_2^{-1}\mu_1 \mu_2^T + \Sigma_2^{-1}\mu_2 \mu_2^T \right\} \right\} \\ & = \frac{1}{2} \left\{ \log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - tr \left\{ \Sigma_1^{-1} \Sigma_1 \right\} + tr(\Sigma_2^{-1}\Sigma_1) + tr \left\{ \mu_1^T\Sigma_2^{-1}\mu_1 - 2 \mu_1^T\Sigma_2^{-1}\mu_2 + \mu_2^T\Sigma_2^{-1}\mu_2 \right\} \right\} \\ & = \frac{1}{2} \left\{ \log\frac{\lvert\Sigma_2 \rvert}{\lvert\Sigma_1 \rvert} - tr \left\{ \Sigma_1^{-1} \Sigma_1 \right\} + tr(\Sigma_2^{-1}\Sigma_1) + (\mu_2 - \mu_1)^T \Sigma_2^{-1}(\mu_2 - \mu_1) \right\} \\ & = \frac{1}{2} \left\{ \log\lvert\Sigma_2 \Sigma_1^{-1} \rvert + tr(\Sigma_2^{-1}\Sigma_1) + (\mu_2 - \mu_1)^T \Sigma_2^{-1}(\mu_2 - \mu_1) - tr(\Sigma_1^{-1} \Sigma_1) \right\}. \end{aligned}\]JS (Jensen-Shannon) Divergence
JS散度是基于KL散度的变形,度量两个概率分布的相似度,解决了KL散度非对称的问题,一般是对称的,取值在0到1之间。
\[D_{JS}(P \Vert Q) = \frac{1}{2} D_{KL}\left( P \bigg\Vert \frac{P + Q}{2} \right) + \frac{1}{2} D_{KL}\left( Q \bigg\Vert \frac{P + Q}{2} \right).\]JS散度性质:
- 对称性。
JS散度局限性:
当两个分布距离很远,完全没有重叠时,JS散度为一个常数,在学习算法中也就意味着这一点的梯度为0,即梯度消失。
Wasserstein Distance
Wasserstein距离度量两个概率分布之间的距离。
\[W(P,Q) = \inf_{\gamma \sim \Pi(P,Q)} \mathbb{E}_{(x,y) \sim \gamma}[\Vert x-y \Vert].\]\(\lambda\)阶Wasserstein距离为:
\[W_\lambda(P,Q) = \left( \inf_{\gamma \sim \Pi(P,Q)} \mathbb{E}_{(x,y) \sim \gamma} \left[\Vert x-y \Vert^\lambda \right] \right)^{1/\lambda}.\]其中,\(\Pi(P,Q)\)是\(P\)和\(Q\)分布组合的所有可能的联合分布的集合,对于可能的联合分布\(\gamma\),从中采样\((x,y)\),得到一个样本,计算这对样本的距离\(\Vert x-y \Vert\),从而可求得该联合分布下样本对之间距离的期望值。从所有可能的联合分布中得到所有可能的样本距离期望值,并取下确界即为Wasserstein距离。
直观理解:样本对之间距离的期望值可以理解为在\(\gamma\)路径规划下把土堆\(P\)推到土堆\(Q\)所需要的消耗,Wasserstein距离就是在最优路径下的最小消耗。因此,Wasserstein距离又称Earth-Mover距离。
Wasserstein距离的优势:
即使两个分布之间重叠很少或没有重叠,仍能反映出两个分布的远近。例如:
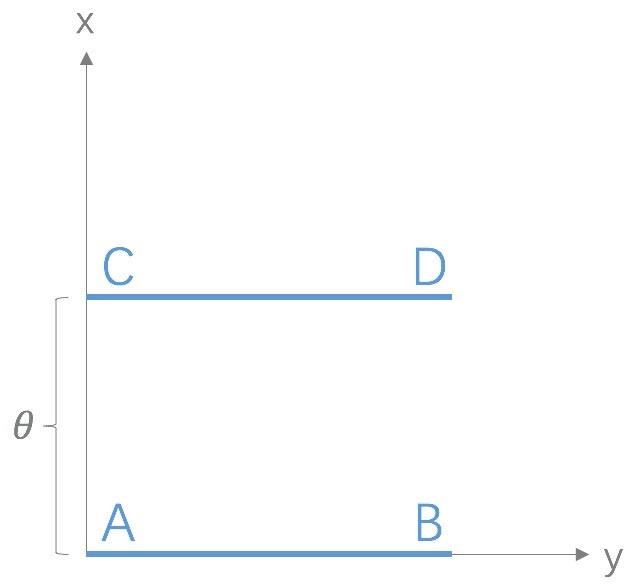
二维空间中的两个分布\(P\)和\(Q\)分别在线段AB和CD上均匀分布,通过调节参数\(\theta\)来控制两个分布的距离远近,则可得到:
\[D_{KL}(P \Vert Q) = \begin{cases} +\infty, & \theta \neq 0 \\ 0, & \theta = 0. \end{cases}\] \[D_{JS}(P \Vert Q) = \begin{cases} \log 2, & \theta \neq 0 \\ 0, & \theta = 0. \end{cases}\] \[W(P,Q) = \vert \theta \vert.\]其中,当两个分布没有重叠时,KL散度和JS散度出现突变,无法反映分布之间的距离信息,而Wasserstein距离则是平滑的,仍能表示两个分布之间的距离远近。如果使用梯度下降的方法来优化参数\(\theta\),则KL散度和JS散度无法提供梯度。因此,Wasserstein距离相对于KL散度和JS散度具有一定的优势和更广的适用范围。
TV (Total Variation) Distance
- A distance measure for probability distributions.
- This is the largest possible difference between the probability distributions.
Definition:
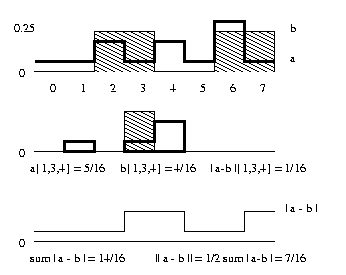
\[D_{TV}(P,Q) = \sup_{x\in X}\lvert P(x) - Q(x) \rvert.\]Relation to KL-divergence:
\[D_{TV}(P,Q) \le \sqrt{\frac{1}{2}D_{KL}(P\Vert Q)}.\]When the set is countable, the TV distance is related to the \(L_1\) norm:
\[D_{TV}(P,Q) = \frac{1}{2}\lVert P-Q \rVert_1 = \frac{1}{2}\sum_{x\in X}\lvert P(x) - Q(x)\rvert.\]