Motivation

  • UAV Applications:
    • Industrial inspection.
    • Search and rescue.
    • Package delivery.
  • To achieve full autonomy in these scenarios, the motion planning module plays an essential role in generating safe and smooth motions.
  • Two critical unsolved issues:
    • No existing works guarantee to generate safe and kinodynamic feasible trajectory at a high success rate with limited time and onboard computing resources.
      • Efficiency and robustness of the trajectory generation are essential.
      • When a quadrotor flying at high speed in unknown environments, trajectories should be re-generated constantly in a very short time to avoid emergent threats.
    • To ensure the kinodynamic feasibility of the generated motions, constraints on the velocity and acceleration are often enforced conservatively.
      • As a result, the aggressiveness of the generated trajectories are often hard to be tuned to satisfy applications where a high flight speed is preferable.
  • Related work:
    • Hard-Constrained methods:
      • Minimum-snap trajectory generation.
        • Represented as piecewise polynomials.
        • Generated by solving a quadratic programming (QP) problem.
      • One common drawback of the methods is that the time allocation of the trajectory is given by naive heuristics.
        • Significantly reduce the quality of the trajectory.
      • Feasible solution can only be obtained by iteratively adding more constraints and solving the QP problem.
        • It is undesirable for real-time application.
      • Ensure global optimality by the convex formulation, but distance to obstacles in the free space is ignored, which often results in trajectories being close to obstacles.
      • Also, the kinodynamic constraints are conservative, making the trajectory’s speed deficient for fast flight.
    • Soft-Constrained methods:
      • Formulate trajectory generation as a non-linear optimization problem.
      • Take smoothness and safety into account.
      • Methods:
        • Generate discrete-time trajectories by minimizing its smoothness and collision cost using gradient descent methods.
        • Also, optimization can be solved by a gradient-free sampling method.
        • Continuous-time polynomial trajectories method is presented to avoid numeric differentiation errors and is more accurate to represent the motions of drones.
          • But it suffers from a low success rate.
        • To increase the success rate, a collision-free initial path firstly using an informed sampling-based path searching method.
          • This path serves as a higher quality initial guess of non-linear optimization and thus improve the success rate.
        • Trajectory is parameterized as a uniform B-spline.
          • B-spline is continuous by nature, which reduce the number of constraints.
          • It is also particularly useful for local replanning thanks to its property of locality.
      • These methods utilize gradient information to push trajectory far from obstacles.
      • But, suffer from local minima and having no strong guarantee of success rate and kinodynamic feasibility.

Contributions

  • Propose a robust and efficient quadrotor motion planning system for fast flight in 3D complex environment.
    • Present a complete and robust online trajectory generation method.
  • Adopt a kinodynamic path searching method to find a safe, kinodynamic feasible, and minimum-time initial trajectory in the discretized control space.
    • Linear quadratic minimum-time control is adopted.
    • The initial path is refined in a carefully designed B-spline optimization.
  • Improve the smoothness and clearance of the trajectory by a B-spline optimization, which incorporates gradient information from a Euclidean distance field and dynamic constraints efficiently utilizing the convex hull property of B-spline.
    • Unlike previous methods in which computational expensive line integrals along the trajectory are calculated.
    • Redesigned to be simpler based on the convex hull property of B-Spline.
    • Improve the computation efficiency and convergent rate.
  • An iterative time adjustment method is adopted to guarantee dynamically feasible and non-conservative trajectories.
    • Squeeze infeasible velocity and acceleration out from the profiles while avoiding constraining them conservatively.
  • Code.
    • ROS package.
  • Video.
  • Compare to existing works:
    • Generate high-quality trajectories in cluttered environments in a much shorter time with a higher success rate.
    • It can generate aggressive motion under the premise of dynamic feasibility.

Method

Kinodynamic path searching

  • Front-end kinodynamic path searching module:
    • Originated from the hybrid-state A* search1.
    • Search for a safe and kinodynamic feasible trajectory that is minimal w.r.t. time duration and control cost in a voxel grid map.
    • Searching loop is similar to the standard A* algorithm.

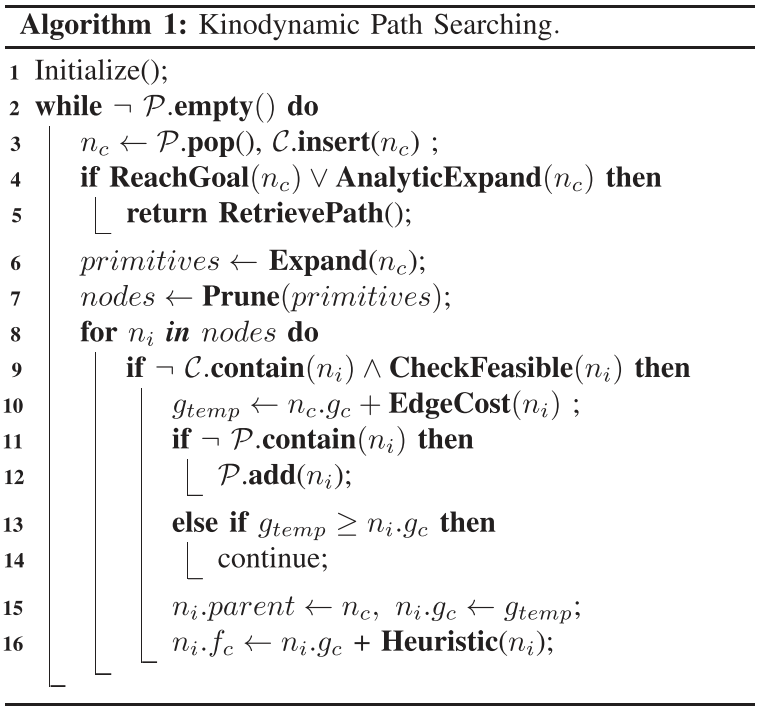
  • \(P\) and \(C\) refer to the open and closed set.
  • Instead of straight lines, motion primitives respecting the quadrotor dynamic are used as graph edge.
  • A structure Node is used to record a primitive.

Primitives Generation

  • Motion primitives used in Expand() function.

The differential flatness of quadrotor systems allows us to represent the trajectory by three independent 1D time-parameterized polynomial functions:

\[\mathbf{p}(t) := [p_x(t), p_y(t), p_z(t)]^T,\] \[p_\mu(t) = \sum_{k=0}^K a_k t^k,\]

where \(\mu \in \{ x,y,z \}\).

Consider the quadrotor as a linear time-invariant (LTI) system.

State vector:

\[\mathbf{x}(t) := [\mathbf{p}(t)^T, \dot{\mathbf{p}}(t)^T, \cdots, \mathbf{p}^{(n-1)}(t)^T]^T \in X \subset \mathbb{R}^{3n}.\]

Control input:

\[\mathbf{u}(t) := \mathbf{p}^{(n)}(t) \in U:=[-u_{max}, u_{max}]^3 \subset \mathbb{R}^3.\]

Then, the state space model can be defined as:

\[\dot{\mathbf{x}} = \mathbf{A}\mathbf{x} + \mathbf{B}\mathbf{u},\] \[\mathbf{A} = \begin{bmatrix} 0 & I_3 & 0 & \cdots & 0 \\ 0 & 0 & I_3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & \cdots & 0 & I_3 \\ 0 & \cdots & \cdots & 0 & 0 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ I_3 \end{bmatrix}.\]

The complete solution for the state equation is expressed as:

\[\mathbf{x}(t) = e^{\mathbf{A}(t)}\mathbf{x}(0) + \int_0^t e^{\mathbf{A}(t - \tau)} \mathbf{B}\mathbf{u}(\tau)d\tau.\]

Then, the trajectory of the quadrotor can be obtained via the initial state \(\mathbf{x}(0)\) and the control input \(\mathbf{u}(t)\).

In Expand():

  • Given the current state of the quadrotor.
  • A set of discretized control inputs \(U_D \subset U\) is applied for duration \(\tau\).
  • In practice, select \(n = 2\), corresponds to a double integrator.
  • Each axis \([-u_{max}, u_{max}]\) is discretized uniformly as \(\left\{ -u_{max}, -\frac{r-1}{r}u_{max}, \cdots, \frac{r-1}{r}u_{max}, u_{max} \right\}\).
  • Thus, results in \((2r+1)^3\) primitives.

Actual Cost and Heuristic Cost

Define the cost (time and control cost) of a trajectory as:

\[J(T) = \int_0^T \Vert \mathbf{u}(t)\Vert^2 dt + \rho T.\]

Then, EdgeCost() calculates the cost of:

  • a motion primitive generated with the discretized input \(\mathbf{u}(t) = \mathbf{u}_d\).
  • and duration \(\tau\) as \(e_c = (\Vert \mathbf{u}_d \Vert^2 + \rho)\tau\).

Actual cost (start \(\to\) current):

  • Use \(g_c\) to represent the actual cost of an optimal path from the start state \(\mathbf{x}_s\) to the current state \(\mathbf{x}_c\).
  • Let the optimal path consists of \(J\) primitives, then:
\[g_c = \sum_{j=1}^J (\Vert \mathbf{u}_{dj}\Vert^2 + \rho)\tau.\]

Heuristic cost (current \(\to\) goal):

  • An admissible and informative heuristic is essential to speed up the searching as in A*.
  • Heuristic():
\[p_\mu^*(t) = \frac{1}{6}\alpha_\mu t^3 + \frac{1}{2}\beta_\mu t^2 + v_{\mu c} + p_{\mu c},\] \[\begin{bmatrix} \alpha_\mu \\ \beta_\mu \end{bmatrix} = \frac{1}{T^3} \begin{bmatrix} -12 & 6T \\ 6T & -2 T^2 \end{bmatrix} \begin{bmatrix} p_{\mu g} - p_{\mu c} - v_{\mu c}T \\ v_{\mu g} - v_{\mu c} \end{bmatrix},\] \[J^*(T) = \sum_{\mu \in \{ x,y,z \}} \left( \frac{1}{3}\alpha_\mu^2 T^3 + \alpha_\mu \beta_\mu T^2 + \beta_\mu^2 T \right),\]

where \(p_{\mu c}, v_{\mu c}, p_{\mu g}, v_{\mu g}\) are the current and goal position and velocity.

To find the optimal time \(T\) that minimize the cost:

  • Substitute \(\alpha_\mu, \beta_\mu\) into \(J^*(T)\).
  • Find the roots of \(\frac{\partial J^*(T)}{\partial T} = 0\).
  • Feasible trajectory is selected and denoted as \(T_h\).
  • Heuristic cost denotes as \(h_c = J^*(T_h)\).

Then,

\[f_c = g_c + h_c = g_c + J^*(T_h).\]

Analytic Expansion

  • Due to the discretized control input, it is difficult to have a primitive end exactly in the goal state.
  • Induce an analytic expansion scheme to compensate for it and also to speed up the searching.

AnalyticExpand():

  • When a node is popped from the open set,
  • if it passes the safety and dynamic feasibility check, the searching is terminated in advance.

The strategy is effective for improving efficiency especially in sparse environments, since

  • it has a higher success rate,
  • and terminates the searching earlier.

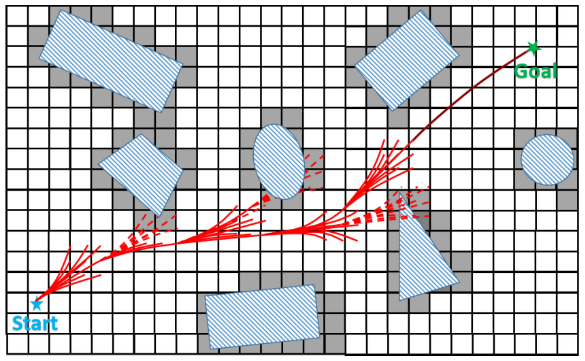
B-spline Trajectory Optimization

  • Drawback of the kinodynamic path searching:
    • The path produced by the kinodynamic path searching can be suboptimal.
    • The path is often close to obstacle since distance information in the free space is ignored.
  • Improve the smoothness and clearance of the path via B-spline optimization.
    • Utilize the convex hull property of uniform B-splines.
    • Incorporate gradient information from the Euclidean distance field and dynamic constraints.
    • It converges within a very short duration to generate smooth, safe and dynamically feasible trajectories.

Uniform B-splines

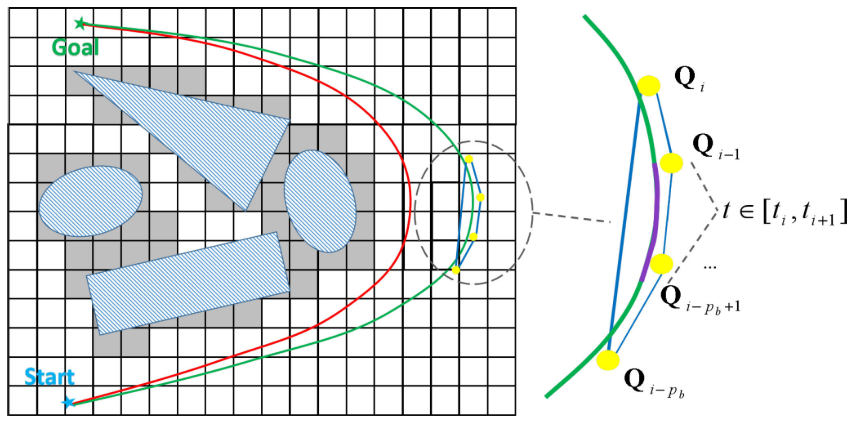
  • A B-spline is a piecewise polynomial uniquely determined by its degree \(p_b\).
  • Control points: \(\{ \mathbf{Q}_0, \mathbf{Q}_1, \cdots, \mathbf{Q}_N \}, \mathbf{Q}_i \in \mathbb{R}^3\).
  • Knot vector: \([t_0, t_1, \cdots, t_M], M = N + p_b + 1, t_m \in \mathbb{R}\).
    • For a uniform B-spline, each knot span \(\Delta t_m = t_{m+1} - t_m\) has identical value \(\Delta t\).
  • A B-spline trajectory is parameterized by time \(t \in [t_{p_b}, t_{M-p_b}]\).
  • The derivative of a B-spline is also a B-spline.

To evaluate the position at time \(t \in [t_m, t_{m+1}) \subset [t_{p_b}, t_{M-p_b}]\), normalize \(t\) as:

\[s(t) = \frac{t-t_m}{\Delta t}.\]

Then, the position can be evaluated using the matrix representation:

\[\mathbf{p}(s(t)) = s(t)^T \mathbf{M}_{p_b+1}\cdot \mathbf{q}_m,\] \[s(t) = [1 \quad s(t) \quad s^2(t) \quad \cdots \quad s^{p_b}(t)]^T,\] \[\mathbf{q}_m = [Q_{m-p_b} \quad Q_{m-p_b+1} \quad Q_{m-p_b+2} \quad \cdots \quad Q_m]^T,\]

where \(\mathbf{M}_{p_b+1}\) is a constant matrix determined by \(p_b = 3\).

Convex Hull Property

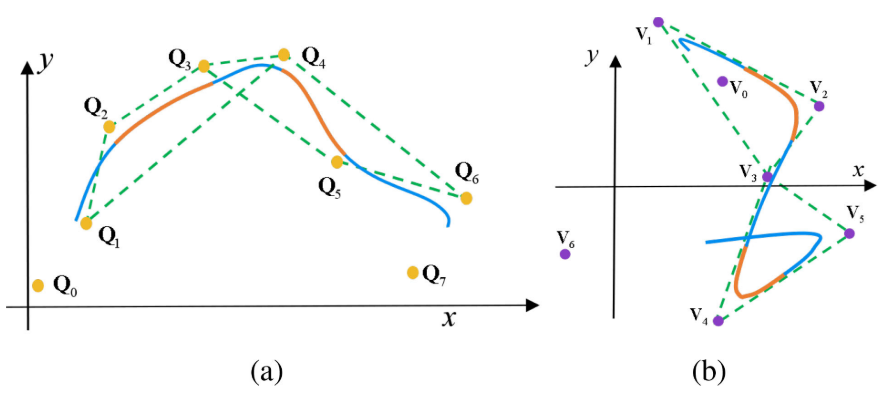
  • This property is extremely useful for ensuring the dynamic feasibility and safety of the entire trajectory.
  • Dynamic feasibility:
    • It suffices to constrain all velocity and acceleration control points.
      • velocity: \(\{ \mathbf{V}_0, \mathbf{V}_1, \cdots, \mathbf{V}_{N-1} \}, \mathbf{V}_i = \frac{1}{\Delta t} (\mathbf{Q}_{i+1} - \mathbf{Q}_i), \mathbf{V}_i \in [-v_{max}, v_{max}]^3\).
      • acceleration: \(\{ \mathbf{A}_0, \mathbf{A}_1, \cdots, \mathbf{A}_{N-2} \}, \mathbf{A}_i = \frac{1}{\Delta t} (\mathbf{V}_{t+1} - \mathbf{V}_i), \mathbf{A}_i \in [-a_{max},a_{max}]^3\).

  • Safety:

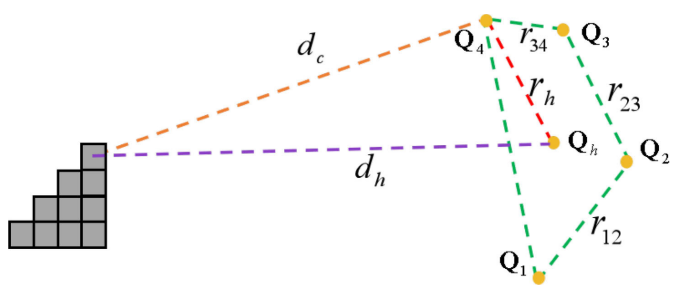
    • Need to ensure that all its convex hulls are collision-free.
      • The distance between any one occupied voxel and any one point \(Q_h\) in the convex hull \(d_h > 0\).
      • \(d_h > d_c - r_h\).
        • \(d_c\): the distance between the voxel and any one control point.
        • \(r_h \le r_{12}+r_{23}+r_{34}\).
        • Then, \(d_h > d_c - (r_{12}+r_{23}+r_{34})\).

Thus, the convex hull is guaranteed to be collision-free if we ensure:

\[d_c > 0, \quad r_{j,j+1} < d_c/3, \quad j \in \{ 1,2,3 \}.\]

Cost Function

  • For a B-spline trajectory:
    • Degree: \(p_b\).
    • Control points: \(\{ Q_0, Q_1, \cdots, Q_N \}\).
    • Optimize the subset of \(N+1-2p_b\) control points: \(\{ Q_{p_b}, Q_{p_b+1}, \cdots, Q_{N-p_b} \}\).
    • The first and last \(p_b\) control points should not be changed because they determine the boundary state.

Define the overall cost function as:

\[f_{total} = \lambda_1 f_s + \lambda_2 f_c + \lambda_3(f_v + f_a),\]

where

  • \(f_s\): smoothness cost.
  • \(f_c\): collision cost.
  • \(f_v\): soft limit on velocity.
  • \(f_a\): soft limit on acceleration.
  • \(\lambda_1,\lambda_2,\lambda_3\): trade off the smoothness, safety, and dynamic feasibility.

Smoothness cost \(f_s\):

  • captures the geometric information of the trajectory.
  • does not depend on time allocation.
    • because that after optimization the time allocation may be adjusted.

Define \(f_s\) via using an elastic band cost function:

\[f_s = \sum_{i = p_b-1}^{N-p_b+1}\Vert \underbrace{(Q_{i+1} - Q_i)}_{F_{i+1,i}} + \underbrace{(Q_{i-1} - Q_i)}_{F_{i-1,i}} \Vert^2.\]

From a physical standpoint:

  • view a trajectory as an elastic band.
  • \(F_{i+1,i}\) and \(F_{i-1,i}\) are the joint force of two springs connecting the nodes \(Q_{t+1},Q_i\) and \(Q_{i-1},Q_i\), respectively.
  • If all terms equal to zero, all the control points would uniform distribute in a straight line, which is ideally smooth.

Collision cost \(f_c\):

  • Formulate as the repulsive force of the obstacles acting on each control point.
\[f_c = \sum_{i=p_b}^{N-p_b}F_c(d(Q_i)),\]

where

  • \(d(Q_i)\) is the distance between \(Q_i\) and the closet obstacle.
  • \(F_c()\) is a differentiable potential cost function.
    • \(d_{thr}\) specifying the threshold of obstacle clearance.
\[F_c(d(Q_i)) = \begin{cases} (d(Q_i) - d_{thr})^2 & d(Q_i) \le d_{thr} \\ 0 & d(Q_i) > d_{thr}. \end{cases}\]

Also, the following euqation must be satisfied so that the trajectory is collision-free:

\[d_c > 0, \quad r_{j,j+1} < d_c/3, \quad j \in \{ 1,2,3 \}.\]
  • \(d_c > 0\) is apparent.
  • In practice, select small \(r_{j,j+1} < 0.2\), the trajectory is safe in most cases.
  • This may be invalid in extreme cases:
    • the environment is very cluttered.
    • in this case, select smaller \(r_{j,j+1}\), the trajectory also can be safe.

Dynamic feasibility cost:

  • penalize velocity or acceleration along the trajectory exceeding maximum allowable value \(v_{max},a_{max}\).

The penalty for \(v_\mu\) is:

\[F_v(v_\mu) = \begin{cases} (v_\mu^2 - v_{max}^2)^2 & v_\mu^2 > v_{max}^2 \\ 0 & v_\mu^2 \le v_{max}^2, \end{cases}\]

where \(\mu \in \{x,y,z\}\).

Then, the dynamic feasibility cost function is defined as:

\[\begin{aligned} f_v & = \sum_{\mu}\sum_{i=p_b-1}^{N-p_b} F_v(V_{i\mu}), \\ f_a & = \sum_{\mu}\sum_{i=p_b-2}^{N-p_b} F_a(A_{i\mu}). \end{aligned}\]

Time Adjustment

  • We have constrained kinodynamic feasibility in the path searching and optimization.
  • However, sometimes we get infeasible trajectories.
  • Reason:
    • gradient information tends to lengthen the overall trajectory while pushing it far from obstacles.
    • Then, the quadrotor has to fly more aggressively in order to travel longer distance within the same time.
    • Unavoidably causes over aggressive motion if the original motion is already near to the physical limits.
  • To guarantee dynamic feasibility:
    • adopt a time adjustment method.
      • based on the relations between the derivatives control points and the time allocation of the non-uniform B-spline.
    • Change the flight aggressiveness as we expected by adjusting the associated time allocation (knot spans).
    • Thus, the dynamic feasibility can be ensured without over-conservative constraints.

Non-Uniform B-spline

  • A more general kind of B-spline.
  • Difference to uniform B-spline:
    • Each of its knot span \(\Delta t_m = t_{m+1}-t_m\) is independent to others.
\[\begin{aligned} \mathbf{V}_i' & = \frac{p_b(Q_{i+1} - Q_i)}{t_{i+p_b+1}-t_{i+1}}, \\ \mathbf{A}_i' & = \frac{(p_b-1)(V_{i+1}' - V_i')}{t_{i+p_b+1} - t_{t+2}}. \end{aligned}\]

Knot Spans Adjustment

Let \(\mathbf{V}_i' = [V_{i,x}', V_{i,y}', V_{i,z}']^T\) be an infeasible control point of velocity.

Let \(V_{i,\mu}'\) be the largest infrasible component and \(\vert V_{i,\mu}' \vert = v_m\).

\(V_{i,\mu}'\) is influenced by the duration \((t_{i+p_b+1} - t_{i+1})\).

If we change the duration as follows:

\[\hat{t}_{i+p_b+1} - \hat{t}_{i+1} = \mu_v(t_{i+p_b+1} - t_{i+1}),\]

where \(\mu_v = \frac{v_m}{v_{max}}\).

Then, the velocity is feasible as:

\[\hat{V}_{i,\mu} = \frac{p_b(Q_{i+1,\mu} - Q_{i,\mu})}{\hat{t}_{i+p_b+1} - \hat{t}_{i+1}} = \frac{1}{\mu_v}V_{i,\mu}' = v_{max}.\]

Similarly, let \(\mu_a = \left( \frac{a_m}{a_{max}} \right)^{\frac{1}{2}}\), then,

\[\hat{A}_{i,\mu} = \frac{1}{\mu_a^2}A_{i,\mu}' = a_{max}.\]

Iterative Time Adjustment

  • It iteratively finds the infeasible velocity and acceleration control points of the trajectory.
  • Adjust the corresponding knot spans.
    • Bounding \(\mu_v', \mu_a'\) with two constant \(\alpha_v,\alpha_a\) slightly larger than \(1\), prevents any time span from being extended excessively.

Experiment

  • C++, NLopt (a general non-linear optimization solver).
  • Parameters:
    • Path searching: \(\gamma = 2, \tau = 0.5\).
    • Optimization: \(\lambda_1 = 10.0, \lambda_2 = 0.8, \lambda_3 = 0.01\).
    • Time adjustment: \(\alpha_v = \alpha_a = 1.1\).
  • Platforms:
    • Autonomous flight quadrotor:
      • Velodyne VLP-16 3D LiDAR. LOAM.
        • estimate the pose of the quadrotor.
        • generate a dense point cloud map.
        • Fuse the laser-based estimation with IMU and sonar measurements by EKF.
      • Intel i7-5500U, 8G RAM, 256G SSD.
        • motion planning.
        • state estimation.
        • mapping.
        • control.
    • Fast-replanning quadrotor:
      • light-weight and agile.
      • OptiTrack.
      • Nvidia TX2.
        • motion planning.
        • control.
  • Experiments:
    • Fast autonomous flight in unknown cluttered environments.
    • Fast-replanning capability in aggressive flight.
  • Re-Planning Strategy:
    • The quadrotor has to re-plan its trajectory frequently in an unknown environment due to the limited sensing range.
    • Receding-Horizon local planning:
      • Trajectories are generated only within the known space.
      • The path searching is terminated once a motion primitive ends outside the range.
      • Then, followed by the optimization and time adjustment.
    • Re-planning triggering mechanism:
      • If the current trajectory collides with newly emergent obstacle.
      • The planner is called at fixed intervals of time.

References

  • B. Zhou, F. Gao, L. Wang, C. Liu, and S. Shen, “Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight,” IEEE RA-L, 2019.

  1. D. Dolgov, S. Thrun, M. Montemerlo, and J. Diebel, “Path planning for autonomous vehicles in unknown semi-structured environments,” IJRR, vol. 29, no. 5, pp. 485–501, 2010. ↩